
【题目】已知F1、F2分别是双曲线![]() 1(a>0,b>0)的左、右焦点,若双曲线的右支上存在一点P,使得(
1(a>0,b>0)的左、右焦点,若双曲线的右支上存在一点P,使得(![]() )
)![]() 0(O为坐标原点),且|PF1|
0(O为坐标原点),且|PF1|![]() |PF2|,则双曲线的离心率的取值范围是_____.
|PF2|,则双曲线的离心率的取值范围是_____.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的半焦距为
的半焦距为![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 有且仅有两个公共点,直线
有且仅有两个公共点,直线![]() 与椭圆
与椭圆![]() 只有一个公共点.
只有一个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点,试问:
两点,试问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出该定值和点
为定值?若存在,求出该定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() 的极值点为
的极值点为![]() ,当
,当![]() 变化时,点(
变化时,点(![]() ,
,![]() )构成曲线M.证明:任意过原点的直线
)构成曲线M.证明:任意过原点的直线![]() ,与曲线M均仅有一个公共点.
,与曲线M均仅有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,对任意
是定义在R上的偶函数,对任意![]() 都有
都有![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() ,给出如下命题:
,给出如下命题:
①![]() ;
;
②直线![]() 是函数
是函数![]() 的图象的一条对称轴;
的图象的一条对称轴;
③函数![]() 在
在![]() 上为增函数;
上为增函数;
④函数![]() 在
在![]() 上有四个零点.
上有四个零点.
其中所有正确命题的序号为( )
A. ①② B. ②④ C. ①②③ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
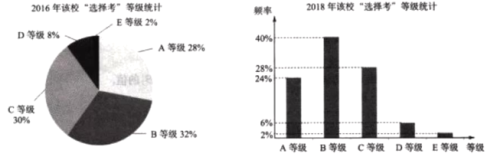
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(x﹣1)﹣lnx(a∈R),g(x)=(1﹣x)ex.
(1)讨论函数f(x)的单调性;
(2)若对任意给定的x0∈[﹣1,1],在区间(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在研究几何时曾定义欧拉三角形,![]() 的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为
的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为![]() 的欧拉三角形.如图,
的欧拉三角形.如图,![]() 是
是![]() 的欧拉三角形(H为
的欧拉三角形(H为![]() 的垂心).已知
的垂心).已知![]() ,
,![]() ,
,![]() ,若在
,若在![]() 内部随机选取一点,则此点取自阴影部分的概率为________.
内部随机选取一点,则此点取自阴影部分的概率为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
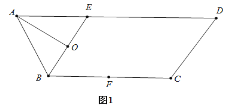
【题目】如图1,等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,O为BE中点,F为BC中点.将
,O为BE中点,F为BC中点.将![]() 沿BE折起到
沿BE折起到![]() 的位置,如图2.
的位置,如图2.
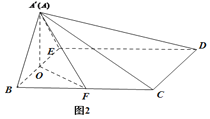
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面BCDE,求点F到平面
平面BCDE,求点F到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com