
【题目】已知函数![]()
⑴若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
⑵若![]() (
(![]() 为自然对数的底数),证明:当
为自然对数的底数),证明:当![]() 时,
时,![]()
【答案】(1)![]() ;
;
(2)见解析.
【解析】
(1)对函数进行求导,由题意可知![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 恒成立,构造新函数令
恒成立,构造新函数令![]() ,求导,研究新函数的单调性,求出新函数的最大值,这样就可以求出实数
,求导,研究新函数的单调性,求出新函数的最大值,这样就可以求出实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,要证
时,要证![]() ,即证
,即证![]() . 又
. 又![]() ,只需证
,只需证![]() ,即证
,即证![]() .
. ![]() ,求导,研究它的单调性,求出它的最小值;设
,求导,研究它的单调性,求出它的最小值;设![]() ,求导,研究它的单调性,求出它的最大值,这样命题得证.
,求导,研究它的单调性,求出它的最大值,这样命题得证.
(1)【解】![]() ,因为函数
,因为函数![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立.
恒成立.
令![]() ,则
,则![]() , 由
, 由![]() ,解得
,解得![]() ,
,
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,则
上单调递减,则![]() , 即
, 即![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
(2)【证明】当![]() 时,要证
时,要证![]() ,即证
,即证![]() .
.
又![]() ,只需证
,只需证![]() ,即证
,即证![]() .
.
设![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]()
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,即
上单调递增,即![]() ,
,
从而有![]() .
.
设![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() ,
,
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减, 即
上单调递减, 即![]() ,
,
从而有![]() .
.
因为![]() 和
和![]() 不同时为0,所以
不同时为0,所以![]() ,故原不等式成立.
,故原不等式成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,![]() ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为![]() 的调查样本,其中城镇户籍与农村户籍各
的调查样本,其中城镇户籍与农村户籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
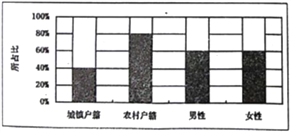
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人员中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为R,则实数m取值范围为
的定义域为R,则实数m取值范围为
A.{m|–1≤m≤0}B.{m|–1<m<0}
C.{m|m≤0}D.{m|m<–1或m>0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为调查会员某年度上半年的消费情况制作了有奖调查问卷发放给所有会员,并从参与调查的会员中随机抽取![]() 名了解情况并给予物质奖励.调查发现抽取的
名了解情况并给予物质奖励.调查发现抽取的![]() 名会员消费金额(单位:万元)都在区间
名会员消费金额(单位:万元)都在区间![]() 内,调查结果按消费金额分成
内,调查结果按消费金额分成![]() 组,制作成如下的频率分布直方图.
组,制作成如下的频率分布直方图.

(1)求该![]() 名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
名会员上半年消费金额的平均值与中位数;(以各区间的中点值代表该区间的均值)
(2)若再从这![]() 名会员中选出一名会员参加幸运大抽奖,幸运大抽奖方案如下:会员最多有两次抽奖机会,每次抽奖的中奖概率均为
名会员中选出一名会员参加幸运大抽奖,幸运大抽奖方案如下:会员最多有两次抽奖机会,每次抽奖的中奖概率均为![]() ,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则会员获得
,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则会员获得![]() 元奖金,不进行第二次抽奖;若正面朝上,会员需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金
元奖金,不进行第二次抽奖;若正面朝上,会员需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金![]() 元,如果未中奖,则所获得的奖金为
元,如果未中奖,则所获得的奖金为![]() 元.若参加幸运大抽奖的会员所获奖金(单位:元)用
元.若参加幸运大抽奖的会员所获奖金(单位:元)用![]() 表示,求
表示,求![]() 的分布列与期望值
的分布列与期望值![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com