
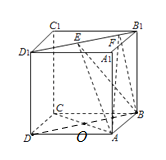
【题目】如图,正方体![]() 棱长为
棱长为![]() ,线段
,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() 平面
平面![]()
B.![]() 始终在同一个平面内
始终在同一个平面内
C.![]() 平面
平面![]()
D.三棱锥![]() 的体积为定值
的体积为定值
【答案】ACD
【解析】
根据题意,依次如图可知![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,通过线面垂直的判定定理可证出
,通过线面垂直的判定定理可证出![]() 平面
平面![]() ,即可证出
,即可证出![]() 平面
平面![]() ,可判断A正确;根据
,可判断A正确;根据![]() ,
,![]() ,
,![]() ,
,![]() 不在一个平面进而断定B错误;由于
不在一个平面进而断定B错误;由于![]() ,根据线面平行的判定,即可判断出C正确;可分别求得
,根据线面平行的判定,即可判断出C正确;可分别求得![]() 和
和![]() ,且
,且![]() 平面
平面![]() ,则求出三棱锥
,则求出三棱锥![]() 的体积,且为定值,即可判断D项正确.
的体积,且为定值,即可判断D项正确.
解:由题可知,正方体![]() 棱长为
棱长为![]() ,
,
则![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
![]() ,
,
连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
而![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
由于是![]() 线段
线段![]() 上的两个动点,则
上的两个动点,则![]()
![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,故选项A正确;
,故选项A正确;
![]() ,
,![]() ,
,![]() 同在平面
同在平面![]() 上,而
上,而![]() 不在平面
不在平面![]() 上,
上,
![]() ,
,![]() 不在同一个平面内,故选项B错误;
不在同一个平面内,故选项B错误;
![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
![]() 平面
平面![]() ,故选项C正确;
,故选项C正确;
由于![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,
由于![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,![]()
![]() ,
,
由于底面积和高都不变,则体积为定值,故选项D正确.
故选:ACD.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ) ![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 经过定点
经过定点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ,若存在,请求出定点
,若存在,请求出定点![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过圆![]() 与
与![]() 轴正半轴的交点A作圆O的切线
轴正半轴的交点A作圆O的切线![]() ,M为
,M为![]() 上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线
上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线![]() 上运动时,△MAQ的垂心的轨迹方程为________.
上运动时,△MAQ的垂心的轨迹方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取. 方案二:不收管理费,每度0.58元.
(1)求方案一收费![]() 元与用电量x (度)之间的函数关系;
元与用电量x (度)之间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家月用电最在什么范围时,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校设计了一个实验考察方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中2道题的便可通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成,考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,椭圆
两点,椭圆![]() 的右顶点为
的右顶点为![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,且定点
,且定点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年3月7日《科学网》刊登“动物可以自我驯化”的文章表明:关于野生小鼠的最新研究,它们在几乎没有任何人类影响的情况下也能表现出进化的迹象——皮毛上白色的斑块以及短鼻子.为了观察野生小鼠的这种表征,从有2对不同表征的小鼠(白色斑块和短鼻子野生小鼠各一对)的实验箱中每次拿出一只,不放回地拿出2只,则拿出的野生小鼠不是同一表征的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com