
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,满足
点,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;
;
(2)![]() 或
或![]() .
.
【解析】
(1)设出右焦点的坐标,通过点到直线距离公式,可以求出![]() 的值,根据已知可知离心率,进而可以求出
的值,根据已知可知离心率,进而可以求出![]() 的值,利用
的值,利用![]() ,可以求出
,可以求出![]() ,最后求出椭圆的标准方程;
,最后求出椭圆的标准方程;
(2)设出直线![]() 交椭圆于
交椭圆于![]() 两点的坐标,利用
两点的坐标,利用![]() ,可以求出两点纵坐标的关系,直线
,可以求出两点纵坐标的关系,直线![]() 的方程与椭圆的方程联立,利用根与系数的关系,可以求出直线
的方程与椭圆的方程联立,利用根与系数的关系,可以求出直线![]() 的斜率,进而求出直线
的斜率,进而求出直线![]() 的方程.
的方程.
(1)设右焦点为![]() ,则
,则![]() ,
,![]() 或
或![]() (舍去).
(舍去).
又离心率![]() ,即
,即![]() ,解得
,解得![]() ,则
,则![]() ,
,
故椭圆的方程为![]() .
.
(2)设![]() ,因
,因![]() ,
,
所以![]() ,
,![]() ①,
①,
易知当直线![]() 的斜率不存在或斜率为0时,①不成立,
的斜率不存在或斜率为0时,①不成立,
于是设![]() 的方程为
的方程为![]() ,联立
,联立![]() 消去
消去![]() 得
得![]() ,
,
因为![]() ,所以直线与椭圆相交.
,所以直线与椭圆相交.
于是![]() ②,
②,![]() ③,
③,
由①②得,![]() ,代入③整理得
,代入③整理得![]() .
.
所以直线![]() 的方程是
的方程是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为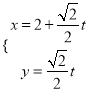 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过圆![]() 与
与![]() 轴正半轴的交点A作圆O的切线
轴正半轴的交点A作圆O的切线![]() ,M为
,M为![]() 上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线
上任意一点,过M作圆O的另一条切线,切点为Q.当点M在直线![]() 上运动时,△MAQ的垂心的轨迹方程为________.
上运动时,△MAQ的垂心的轨迹方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:![]() -y+3+
-y+3+![]() =0和圆
=0和圆![]() :
:![]() +
+![]() +8x+F=0.若直线l被圆
+8x+F=0.若直线l被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设圆![]() 和x轴相交于A,B两点,点P为圆
和x轴相交于A,B两点,点P为圆![]() 上不同于A,B的任意一点,直线PA,PB交y轴于M,N两点.当点P变化时,以MN为直径的圆
上不同于A,B的任意一点,直线PA,PB交y轴于M,N两点.当点P变化时,以MN为直径的圆![]() 是否经过圆
是否经过圆![]() 内一定点?请证明你的结论;
内一定点?请证明你的结论;
(3)若△RST的顶点R在直线x=-1上,点S,T在圆![]() 上,且直线RS过圆心
上,且直线RS过圆心![]() ,∠SRT=
,∠SRT=![]() ,求点R的纵坐标的范围.
,求点R的纵坐标的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取. 方案二:不收管理费,每度0.58元.
(1)求方案一收费![]() 元与用电量x (度)之间的函数关系;
元与用电量x (度)之间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家月用电最在什么范围时,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校设计了一个实验考察方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中2道题的便可通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成,考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校初中部共120名教师,高中部共180名教师,其性别比例如图所示,已知按分层抽样方法得到的工会代表中,高中部女教师有6人,则工会代表中男教师的总人数为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com