
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 依题意,得${2}^{n+1}{a}_{n+1}-{2}^{n}{a}_{n}=1$,可判断出数列{2nan}为公差是1的等差数列,进一步可求得21a1=2,即其首项为2,从而可得an=$\frac{n+1}{{2}^{n}}$,继而可得答案.
解答 解:∵${2^n}{a_n}={2^{n+1}}{a_{n+1}}-1$,即${2}^{n+1}{a}_{n+1}-{2}^{n}{a}_{n}=1$,
∴数列{2nan}为公差是1的等差数列,
又a1=1,
∴21a1=2,即其首项为2,
∴2nan=2+(n-1)×1=n+1,
∴an=$\frac{n+1}{{2}^{n}}$.
∴a1=1,a2=$\frac{3}{4}$,a3=$\frac{1}{2}$,a4=$\frac{5}{16}$>$\frac{1}{5}$,a5=$\frac{6}{32}$=$\frac{3}{16}$<$\frac{3}{15}$=$\frac{1}{5}$,
∴若${a_n}<\frac{1}{5}$,则n的最小值为5,
故选:B.
点评 本题考查数列递推式,判断出数列{2nan}为公差是1的等差数列,并求得an=$\frac{n+1}{{2}^{n}}$是关键,考查分析应用能力.属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:解答题
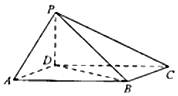 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
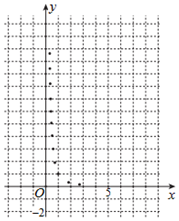 某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).
某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数x与烧开一壶水所用时间y的一组数据,且作了一定的数据处理(如表),得到了散点图(如图).| $\bar x$ | $\bar y$ | $\bar w$ | $\sum_{i=1}^{10}{({x_i}-\bar x)^2}$ | $\sum_{i=1}^{10}{({w_i}-\bar w)^2}$ | $\sum_{i=1}^{10}({x_i}-\bar x)({y_i}-\bar y)$ | $\sum_{i=1}^{10}({w_i}-\bar w)({y_i}-\bar y)$ |
| 1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ac2>bc2 | C. | 2-a<2-b | D. | lga>lgb |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com