【题目】设等差数列
的前
项和为
，数列
的前项和为
，下列说法错误的是（ ）
A. 若有最大值，则也有最大值
B. 若有最大值，则也有最大值
C. 若数列
不单调，则数列
也不单调
D. 若数列不单调，则数列也不单调
【答案】C
【解析】
根据等差数列的性质知数列{a2n﹣1}的首项是a1，公差为2d，结合等差数列的前n项和公式以及数列的单调性和最值性与首项公差的关系进行判断即可．
解：数列{a2n﹣1}的首项是a1，公差为2d，
A．若Sn有最大值，则满足a1＞0，d＜0，则2d＜0，即Tn也有最大值，故A正确，
B．若Tn有最大值，则满足a1＞0，2d＜0，则d＜0，即Sn也有最大值，故B正确，
C．Sn＝na1
d
n2+（a1
）n，对称轴为n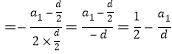
，
Tn＝na12d＝dn2+（a1﹣d）n，对称轴为n
，
不妨假设d＞0，
若数列{Sn}不单调，此时对称轴n
，即
1，
此时Tn的对称轴n
1，则对称轴
有可能成立，此时数列{Tn}有可能单调递增，
故C错误，
D．不妨假设d＞0，若数列{Tn}不单调，此时对称轴n
，即2，
此时{Sn}的对称轴n
2
，即此时{Sn}不单调，故D正确
则错误是C，
故选：C．/span>
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某校高二（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，且将全班25人的成绩记为
由右边的程序运行后,输出
.据此解答如下问题：
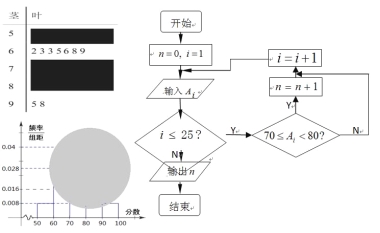
（Ⅰ）求茎叶图中破损处分数在[50，60），[70，80），[80，90）各区间段的频数；
（Ⅱ）利用频率分布直方图估计该班的数学测试成绩的众数，中位数分别是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解一家企业生产的某类产品的使用寿命(单位：小时)，现从中随机抽取一定数量的产品进行测试，绘制频率分布直方图如图所示.
(1)假设同一组中的每个数据可用该组区间的中点值代替，估算这批产品的平均使用寿命；
(2)已知该企业生产的这类产品有甲、乙两个系列，产品使用寿命不低于60小时为合格，合格产品中不低于90小时为优异，其余为一般.现从合格产品中，用分层抽样的方法抽取70件，其中甲系列有35件(1件优异).请完成下面的列联表，并根据列联表判断能否有
的把握认为产品优异与系列有关？
甲系列 | 乙系列 | 合计 | |
优异 | |||
一般 | |||
合计 |
参考数据：
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：
，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种产品的质量以其质量指标值来衡量，质量指标值越大表明质量越好，且质量指标值大于或等于
的产品为优质产品.现用两种新配方（分别称为
配方和
配方）做试验，各生产了 件这种产品，并测量了每件产品的质量指标值（都在区间
内），将这些数据分成
组：
，
，
，
，得到如下两个频率分布直方图：
已知这
种配方生产的产品利润
（单位：百元）与其质量指标值
的关系式均为
.
若以上面数据的频率作为概率，分别从用 配方和 配方生产的产品中随机抽取一件，且抽取的这 件产品相互独立，则抽得的这两件产品利润之和为
的概率为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
过点
，且离心率为
.过抛物线
上一点
作
的切线
交椭圆
于
，
两点.
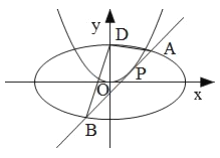
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在直线，使得
，若存在，求出的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数集
由实数构成，且满足：若
（
且
），则
.
（1）若
，试证明中还有另外两个元素；
（2）集合是否为双元素集合，并说明理由；
（3）若中元素个数不超过8个，所有元素的和为
，且中有一个元素的平方等于所有元素的积，求集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
