
分析 求出原函数的导函数,得到函数在(0,+∞)上的单调性,由此求得函数的值域.
解答 解:由f(x)=$\frac{x}{e^x}$,得f′(x)=$\frac{{e}^{x}-x{e}^{x}}{{e}^{2x}}=\frac{1-x}{{e}^{x}}$,
∴当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,
∴f(x)(0,1)上为增函数,在(1,+∞)上为减函数,
则f(x)在(0,+∞)上的最大值为f(1)=$\frac{1}{e}$,
又当x→0时f(x)→0,当x→+∞时,f(x)→0,
∴函数f(x)=$\frac{x}{e^x}$的值域为$(0,\frac{1}{e}]$.
故答案为:$(0,\frac{1}{e}]$.
点评 本题考查函数值域的求法,训练了利用导数研究函数的单调性,是中档题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
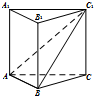 如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.
如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10+2$\sqrt{10}$ | B. | 10+$\sqrt{10}$ | C. | 10-2$\sqrt{10}$ | D. | 10-$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A. | (2,2) | B. | ($\frac{3}{2},2$) | C. | ( $\frac{3}{2},4$) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是最小正周期为π的偶函数 | |
| B. | f(x)的一条对称轴是 $x=\frac{π}{3}$ | |
| C. | f(x)的最大值为2 | |
| D. | 将函数$y=\sqrt{3}sin2x$的图象向左平移$\frac{π}{6}$个单位得到函数f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com