
【题目】已知椭圆![]() 过点
过点![]() ,
,![]() 为
为![]() 内一点,过点
内一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() ,
,![]() 为坐标原点,当
为坐标原点,当![]() 时,
时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先由椭圆![]() 过点
过点![]() 得出
得出![]() 值,再由
值,再由![]() 可得出点
可得出点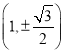 在椭圆上,代入椭圆方程可得出
在椭圆上,代入椭圆方程可得出![]() 的值,即可得出椭圆
的值,即可得出椭圆![]() 的方程;
的方程;
(2)当直线![]() 斜率为0时,易得
斜率为0时,易得![]() ;当直线
;当直线![]() 斜率不为0时,设直线
斜率不为0时,设直线![]() 的方程为
的方程为![]() ,并设点
,并设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,并列出韦达定理,由
的方程联立,并列出韦达定理,由![]() 可得
可得![]() ,由已知条件得
,由已知条件得![]() ,将关系式代入韦达定理并消去
,将关系式代入韦达定理并消去![]() ,于是可得出
,于是可得出![]() 的不等式,即可求出
的不等式,即可求出![]() 的取值范围.
的取值范围.
解:(1)由于![]() ,则
,则![]() 、
、![]() 、
、![]() 三点共线,当
三点共线,当![]() 时,则
时,则![]() ,
,
因为![]() ,
,
所以点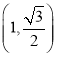 和点
和点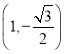 在椭圆上,
在椭圆上,
因为椭圆![]() 过点
过点![]() ,则
,则![]() ,
,
将点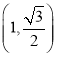 的坐标代入椭圆的方程得
的坐标代入椭圆的方程得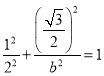 ,解得
,解得![]() ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)当直线![]() 斜率为0时,直线
斜率为0时,直线![]() 的方程为
的方程为![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ;
;
当直线![]() 斜率不为0时,设直线
斜率不为0时,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线![]() 的方程代入椭圆
的方程代入椭圆![]() 的方程并化简得
的方程并化简得![]() ,
,
由韦达定理可得![]() ,
,![]() ,
,
因为![]() ,
,![]() ,且
,且![]() ,
,
所以![]() ,则
,则![]() ,由于
,由于![]() ,所以
,所以![]() ,
,
所以![]() ,则
,则![]() ,
,
由![]() ,
,
上述两式相除得![]() ,
,
由于![]() ,化简得
,化简得![]() ,解得
,解得![]() ,
,
所以![]() ,
,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中无理数
,其中无理数![]() .
.
(Ⅰ)若函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的极值点有三个,最小的记为
的极值点有三个,最小的记为![]() ,最大的记为
,最大的记为![]() ,若
,若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:①命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”;②“
”;②“![]() ”是“
”是“![]() ”的充分不必要条件; ③若
”的充分不必要条件; ③若![]() 为假命题,则
为假命题,则![]() 均为假命题;④对于命题
均为假命题;④对于命题![]() 使得
使得![]() ,则
,则![]() 为
为![]() ,均有
,均有![]() .其中,真命题的个数是 ( )
.其中,真命题的个数是 ( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行了一次创新作文大赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在![]() 之间,其得分的频率分布直方图如图,则下列结论错误的是( )
之间,其得分的频率分布直方图如图,则下列结论错误的是( )
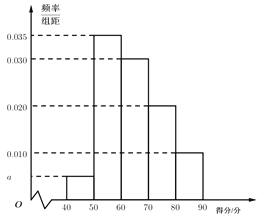
A.得分在![]() 之间的共有40人
之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在![]() 的概率为0.5
的概率为0.5
C.估计得分的众数为55
D.这100名参赛者得分的中位数为65
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex![]() (x﹣a)2+4.
(x﹣a)2+4.
(1)若f(x)在(﹣∞,+∞)上单调递增,求a的取值范围;
(2)若x≥0,不等式f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为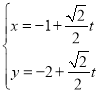 (t为参数),l与C交于A,B两点.
(t为参数),l与C交于A,B两点.
(1)求C的直角坐标方程和l的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比数列,求a的值.
成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将![]() 地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
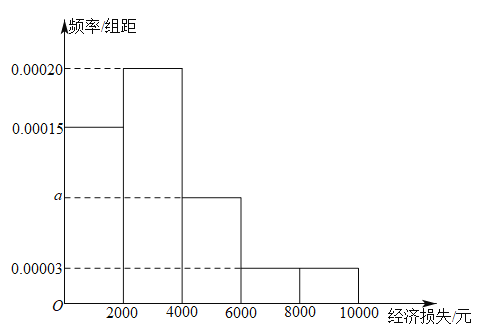
(1)求![]() 的值;
的值;
(2)求![]() 地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出![]() 地区200家实体店经济损失的平均数
地区200家实体店经济损失的平均数![]() 与6000的大小关系.
与6000的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com