
 如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P、Q分别在棱DD1,BC上,BQ=4.
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P、Q分别在棱DD1,BC上,BQ=4.分析 (1)在AA1上取一点N,使得AN=$\frac{2}{3}$AA1,由已知可证四边形BQPN为平行四边形,从而证明PQ∥BN,即可判定PQ∥ABB1A1.
(2)取A1A的中点M,连接PM,BM,PC,可证PM∥BC,又由BC⊥AB,BC⊥A1A,可证BC⊥AB1,由tan∠ABM=tan∠A1AB1,可得∠ABM=∠A1AB1,证明AB1⊥BM,从而可证AB1⊥平面PBC.
解答 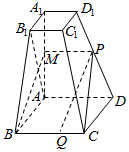 证明:(1)在AA1上取一点N,使得AN=$\frac{2}{3}$AA1,
证明:(1)在AA1上取一点N,使得AN=$\frac{2}{3}$AA1,
∵DP=$\frac{2}{3}$DD1,且A1D1=3,AD=6,
∴PN$\stackrel{∥}{=}$$\frac{2}{3}$AD,又BQ$\stackrel{∥}{=}$$\frac{2}{3}$AD,
∴PN$\stackrel{∥}{=}$BQ,
∴四边形BQPN为平行四边形,
∴PQ∥BN,
∵BN?平面ABB1A1,PQ?ABB1A1.
∴PQ∥ABB1A1.…6分
(2)如图所示,取A1A的中点M,连接PM,BM,PC,
∵A1,A,D1D是梯形的两腰,P是D1D的中点,
∴PM∥AD,于是由AD∥BC知,PM∥BC,
∴P,M,B,C四点共面,
由题设可知,BC⊥AB,BC⊥A1A,
∴BC⊥平面ABB1A1,
∴BC⊥AB1,①
∵tan∠ABM=$\frac{AM}{AB}$=$\frac{3}{6}$=$\frac{{A}_{1}{B}_{1}}{{A}_{1}A}$=tan∠A1AB1,
∴∠ABM=∠A1AB1,
∴∠ABM+∠BAB1=∠A1AB1+∠BAB1=90°,
∴AB1⊥BM,
再由①与BC∩BM=B,知AB1⊥平面PBC.…12分
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了转化思想和数形结合思想,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、③都可能为分层抽样 | D. | ①、④都可能为系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
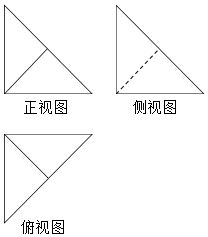 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (60,96) | B. | (45,72) | C. | (30,48) | D. | (15,24) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com