练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．某初级中学有学生111人，其中一年级108人，二、三年级各81人，现要利用抽样方法取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1，2，…，270；使用系统抽样时，将学生统一随机编号1，2，…，270，并将整个编号依次分为10段  如果抽得号码有下列四种情况：
    ①7，34，61，88，115，142，169，196，223，250；
    ②5，9，100，107，111，121，180，195，200，265；
    ③11，38，65，92，119，146，173，200，227，254；
    ④30，57，84，111，138，165，192，219，246，270；
    关于上述样本的下列结论中，正确的是（　　）
    A．②、③都不能为系统抽样B．②、④都不能为分层抽样
    C．①、③都可能为分层抽样D．①、④都可能为系统抽样

    分析 根据所给的四组数据的特点，结合系统抽样中各数据的间隔是相等的，简单随机抽样与分层抽样没有这一明显特征，即可得出结论．

    解答 解：观察所给的四组数据，
    ①，③两组数据中的分段间隔相等，可能是系统抽样或分层抽样，
    ②该组数据中各数据的间隔没有规律，应是简单随机抽样，
    ④该组数据中分段间隔没有规律，应该不是系统抽样和分层抽样．
    由此，符合题意的是选项C．
    故选：C．

    点评 本题考查了简单随机抽样与系统抽样、分层抽样方法的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知数列{an}中，a1=2，an=3an-1+2（n≥2，n∈N*），数列{bn}中，bn=an+1．
    （Ⅰ）证明数列{bn}是等比数列，并求其通项公式；
    （Ⅱ）若cn=$\frac{{b}_{n}}{（{b}_{n}+1）（{b}_{n}+3）}$，求数列{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．经过点P（0，-1）作直线l，若直线l与连接A（1，-2），B（2，1）的线段没有公共点，则直线l的斜率k与倾斜角α的取值范围分别是（　　）
    A．（-∞，-1）∪（1，+∞），（$\frac{π}{4}$，$\frac{3π}{4}$）B．（-∞，-1）∪（1，+∞），（$\frac{π}{4}$，$\frac{π}{2}$）∪（$\frac{π}{2}$，$\frac{3π}{4}$）
    C．（-1，1），[$\frac{π}{4}$，$\frac{3π}{4}$]D．（-1，1），[0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若f（2x）=3x2+1，则函数f（4）=13．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．定义在N*的函数f（x）满足f（1）=2且有f（n+1）=$\left\{\begin{array}{l}\frac{1}{2}f（n），n为偶数\\ f（n），n为奇数\end{array}$，则f（12）的值为（　　）
    A．$\frac{1}{32}$B．$\frac{1}{16}$C．$\frac{1}{64}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．如图，已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形，AA1=6，且A1A⊥底面ABCD，点P、Q分别在棱DD1，BC上，BQ=4．
    （1）若DP=$\frac{2}{3}$DD1，证明：PQ∥平面ABB1A1；
    （2）若P是D1D的中点，证明：AB1⊥平面PBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．幂函数y=x3在[1，2]上的最大值与最小值之和为（　　）
    A．10B．9C．8D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=60°，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）
    A．1B．2C．$\sqrt{3}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．算法程序框图如图所示，若$a=\frac{π}{2}$，$b={3^{\frac{1}{3}}}$，$c={（{\sqrt{e}}）^{ln3}}$，则输出的结果是（　　）
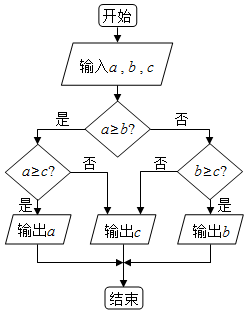
    A．$\frac{a+b+c}{3}$B．aC．bD．c

    查看答案和解析>>

    同步练习册答案