Question

13．经过点P（0，-1）作直线l，若直线l与连接A（1，-2），B（2，1）的线段没有公共点，则直线l的斜率k与倾斜角α的取值范围分别是（　　）

• A． （-∞，-1）∪（1，+∞），（$\frac{π}{4}$，$\frac{3π}{4}$）
• B． （-∞，-1）∪（1，+∞），（$\frac{π}{4}$，$\frac{π}{2}$）∪（$\frac{π}{2}$，$\frac{3π}{4}$）
• C． （-1，1），[$\frac{π}{4}$，$\frac{3π}{4}$]
• D． （-1，1），[0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，0）

Answer 1

分析 由题意画出图形，数形结合求出使直线l与线段AB有公共点的直线l的斜率的范围与倾斜角的范围，然后利用补集思想得答案．

解答 解：如图，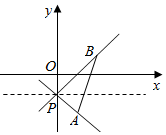

∵A（1，-2），B（2，1），P（0，-1），
∴${k}_{PA}=\frac{-2-（-1）}{1-0}=-1$，${k}_{PB}=\frac{-1-1}{-0-2}=1$，
则使直线l与线段AB有公共点的直线l的斜率的范围为[-1，1]，倾斜角的范围为[0，$\frac{π}{4}$]∪[$\frac{3π}{4}，π$）．
由补集思想可得，直线l与连接A，B的线段没有公共点的斜率的范围为（-∞，-1）∪（1，+∞），
直线的倾斜角的范围为（$\frac{π}{4}$，$\frac{3π}{4}$）．
故选：A．

点评 本题考查直线的倾斜角，考查了直线的倾斜角和斜率的关系，体现了数形结合的解题思想方法，是中档题．