Question

2．在一次数学测验后，数学老师将某班全体学生（50人）的数学成绩进行初步统计后交给其班主任（如表）．

分数	50～60	60～70	70～80	80～90	90～100
人数	2	6	10	20	12

请你帮助这位班主任完成下面的统计分析工作：
（1）列出频率分布表；
（2）画出频率分布直方图及频率分布折线图；
（3）从频率分布直方图估计出该班同学成绩的众数、中位数和平均数．

Answer 1

分析 （1）计算对应的频率，列出频率分布表即可；
（2）根据频率分布表，即可画出频率分布直方图及频率分布折线图；
（3）根据频率分布直方图计算众数、中位数与平均数．

解答 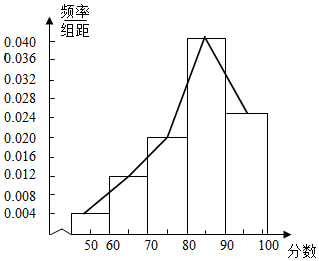解：（1）计算对应的频率，列出频率分布表，如下；…（2分）

分组	频数	频率
[50，60）	2	0.04
[60，70）	6	0.12
[70，80）	10	0.20
[80，90）	20	0.40
[90，100]	12	0.24
合  计	50	1.00

（2）根据频率分布表，画出频率分布直方图及频率分布折线图，如下；…（6分）

（3）根据频率分布直方图知，最高的一组数据[80，90），
所以众数为：$\frac{80+90}{2}$=85；
又0.04+0.12+0.20=0.36＜0.5，
0.36+0.4=0.76＞0.5，
所以中位数在[80，90）内，设为x，
则0.36+（x-80）×0.040=0.5，
解得x=83.5，
即中位数为83.5；
平均数为55×0.04+65×0.12+75×0.20+85×0.40+95×0.24=81.8．…（12分）

点评 本题考查了样本频率分布表、直方图和折线图，以及 众数、中位数和平均数的计算问题，是基础题目．