
| A. | $({\frac{1}{3},1})$ | B. | $({-∞,\frac{1}{3}})∪({1,+∞})$ | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | $({-∞,-\frac{1}{3}})∪({\frac{1}{3},+∞})$ |
分析 分析函数的奇偶性和单调性,进而可将f(x)>f(2x-1)化为:|x|>|2x-1|,即x2>(2x-1)2,解得答案.
解答 解:函数f(x)=31+|x|-$\frac{1}{{1+{x^2}}}$为偶函数,
当x≥0时,f(x)=31+x-$\frac{1}{{1+{x^2}}}$
∵此时y=31+x为增函数,y=$\frac{1}{{1+{x^2}}}$为减函数,
∴当x≥0时,f(x)为增函数,
则当x≤0时,f(x)为减函数,
∵f(x)>f(2x-1),
∴|x|>|2x-1|,
∴x2>(2x-1)2,
解得:x∈$({\frac{1}{3},1})$,
故选:A.
点评 本题考查的知识点是分段函数的应用,函数的奇偶性,函数的单调性,难度中档.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),x∈(-1,1)\\-{x^2}+4x-4,x∈[1,+∞)\end{array}$
已知函数f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),x∈(-1,1)\\-{x^2}+4x-4,x∈[1,+∞)\end{array}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-9,+∞) | D. | (-∞,-9) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
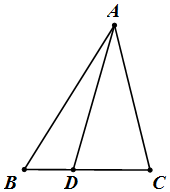 在△ABC中,D为BC边上的动点,且AD=3,B=$\frac{π}{3}$.
在△ABC中,D为BC边上的动点,且AD=3,B=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{25}$ | B. | $\frac{25}{36}$ | C. | $\frac{31}{48}$ | D. | $\frac{49}{64}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com