Question

20．某几何体的三视图如图所示，已知三视图中的圆的半径均为2，则该几何体的体积为（　　）

• A． $\frac{20π}{3}$
• B． 12π
• C． $\frac{44π}{3}$
• D． 16π

Answer 1

分析 由已知中的三视图，可知该几何体是一个球有两处挖去球的八分之一后，在上面放两个半径为2的四分之一的圆柱，所以几何体的体积是${V}_{球}×\frac{3}{4}+\frac{1}{2}{V}_{柱}$即得．

解答 解：由已知中的三视图，可知该几何体是一个球有两处挖去球的八分之一后，在上面放两个半径为2的四分之一的圆柱，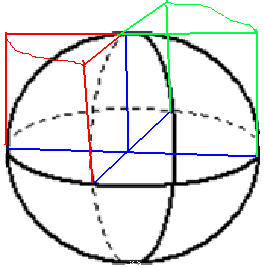
那么：${V}_{球}=\frac{4}{3}π{R}^{3}=\frac{32π}{3}$，
两处挖去球的八分之一，即挖去了$\frac{1}{4}{V}_{球}=\frac{8π}{3}$．
放两个半径为2的四分之一的圆柱，$\frac{1}{2}{V}_{柱}=\frac{1}{2}×π{R}^{2}×h=4π$
所以几何体的体积是${V}_{球}×\frac{3}{4}+\frac{1}{2}{V}_{柱}$=8π+4π=12π．
故选B．

点评 本题考查的知识点是由三视图求体积，解决本题的关键是得到该几何体的形状．属于中档题．