
 如图,某快递公司送货员从公司A处准备开车送货到某单位B处,有A→C→D→B,A→E→F→B两条路线.若该地各路段发生堵车与否是相互独立的,且各路段发生堵车事件的概率如图所示(例如A→C→D算作两个路段;路段AC发生堵车事件的概率为$\frac{1}{6}$,路段CD发生堵车事件的概率为$\frac{1}{10}$).
如图,某快递公司送货员从公司A处准备开车送货到某单位B处,有A→C→D→B,A→E→F→B两条路线.若该地各路段发生堵车与否是相互独立的,且各路段发生堵车事件的概率如图所示(例如A→C→D算作两个路段;路段AC发生堵车事件的概率为$\frac{1}{6}$,路段CD发生堵车事件的概率为$\frac{1}{10}$).分析 (1)由对立事件概率计算公式,分别计算路线A→E→F→B途中堵车概率、路线A→C→D→B途中堵车概率,由此能求出选择路线路线A→E→F→B的途中发生堵车的概率最小.
(2)由题意,ξ可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的数学期望Eξ.
解答 解:(1)由已知得:路线A→E→F→B途中堵车概率为:1-$\frac{4}{5}×\frac{5}{6}×\frac{4}{5}$=$\frac{7}{15}$,
路线A→C→D→B途中堵车概率为:1-$\frac{5}{6}×\frac{9}{10}×\frac{3}{5}$=$\frac{11}{20}$,
所以选择路线路线A→E→F→B的途中发生堵车的概率最小;
由题意,ξ可能取值为0,1,2,3.
P(ξ=0)=$\frac{4}{5}×\frac{5}{6}×\frac{4}{5}$=$\frac{8}{25}$,
P(ξ=1)=$\frac{1}{5}×\frac{5}{6}×\frac{4}{5}+\frac{4}{5}×\frac{1}{6}×\frac{4}{5}+\frac{4}{5}×\frac{5}{6}×\frac{1}{5}$=$\frac{28}{75}$,
P(ξ=2)=$\frac{1}{5}×\frac{1}{6}×\frac{4}{5}+\frac{1}{5}×\frac{5}{6}×\frac{1}{5}+\frac{4}{5}×\frac{1}{6}×\frac{1}{5}$=$\frac{13}{150}$,
P(ξ=3)=$\frac{1}{5}×\frac{1}{6}×\frac{1}{5}$=$\frac{1}{150}$.
ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{8}{25}$ | $\frac{28}{75}$ | $\frac{13}{150}$ | $\frac{1}{150}$ |
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法,考查学生的计算能力,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
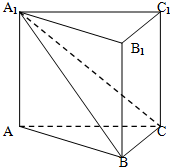 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | $h(t)=-8sin\frac{π}{6}t+10$ | B. | $h(t)=-8cos\frac{π}{6}t+10$ | C. | $h(t)=-8sin\frac{π}{6}t+8$ | D. | $h(t)=-8cos\frac{π}{6}t+8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,正视图,侧视图,俯视图都是边长为1的正方形,则此几何体的外接球和内接球的半径分别为( )
某几何体的三视图如图所示,正视图,侧视图,俯视图都是边长为1的正方形,则此几何体的外接球和内接球的半径分别为( )| A. | $\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{2}$,$\frac{\sqrt{6}}{12}$ | C. | $\frac{\sqrt{6}}{4}$,$\frac{\sqrt{6}}{12}$ | D. | $\frac{\sqrt{6}}{4}$,$\frac{\sqrt{3}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com