
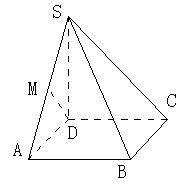
如图,S是正方形ABCD所在平面外一点,且SD⊥面ABCD ,AB=1,SB=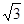 .
.
(1)求证:BC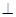 SC;
SC;
(2) 设M为棱SA中点,求异面直线DM与SB所成角的大小
(3) 求面ASD与面BSC所成二面角的大小;
(1) 先证BC⊥平面SDC (2) 异面直线DM与SB所成的角为90°(3) 面ASD与面BSC所成
的二面角为45°
解析试题分析:(1)∵底面ABCD是正方形,∴BC⊥DC.
∵SD⊥底面ABCD,∴SD⊥BC,又DC∩SD=D,
∴BC⊥平面SDC,∴BC⊥SC.
(2)取AB中点P,连结MP,DP.
在△ABS中,由中位线定理得MP//SB, 或其补角为所求.
或其补角为所求. ,又
,又
∴在△DMP中,有DP2=MP2+DM2, 
即异面直线DM与SB所成的角为90°. 
(3).∵SD⊥底面ABCD,且ABCD为正方形,
∴可把四棱锥S—ABCD补形为长方体A1B1C1S—ABCD,
如图2,面ASD与面BSC所成的二面角就是面ADSA1与面
BCSA1所成的二面角,
∵SC⊥BC,BC//A1S, ∴SC⊥A1S,
又SD⊥A1S,∴∠CSD为所求二面角的平面角.
在R t△SCB中,由勾股定理得SC=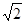 ,在R t△SDC中,
,在R t△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角为45°.
考点:二面角的平面角及求法;异面直线及其所成的角.
点评:本题考查异面直线垂直的证明,考查异面直线所成角的大小的求法,考查二面角的大小的求法,解题
时要认真审题,仔细解答,注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
设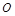 为正方形
为正方形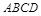 的中心,四边形
的中心,四边形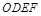 是平行四边形,且平面
是平行四边形,且平面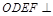 平面
平面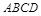 ,若
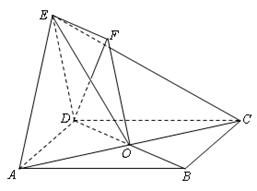
,若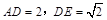 .
.
(1)求证: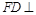 平面
平面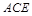 .
.
(2)线段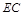 上是否存在一点
上是否存在一点 ,使
,使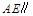 平面
平面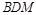 ?若存在,求
?若存在,求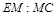 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
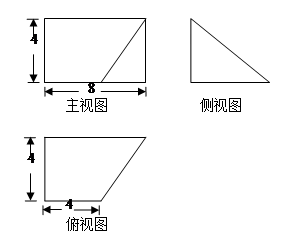
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形
(1)求证: ; (2)求证:
; (2)求证: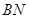
 ;
;
(3)设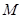 为
为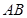 中点,在
中点,在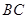 边上找一点
边上找一点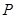 ,使
,使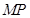
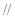 平面
平面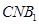 ,并求
,并求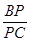 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图。在直三棱柱ABC—A1B1C1中,AB=BC=2AA1,∠ABC=90°,M是BC中点。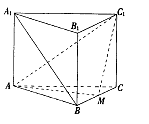
(I)求证:A1B∥平面AMC1;
(II)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位置;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥P-ABC中, AB="AC=4," D、E、F分别为PA、PC、BC的中点, BE="3," 平面PBC⊥平面ABC, BE⊥DF.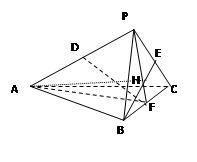
(Ⅰ)求证:BE⊥平面PAF;
(Ⅱ)求直线AB与平面PAF所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方体ABCD—A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.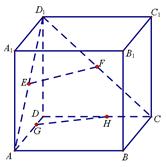
(1)求GH长的取值范围;
(2)当GH取得最小值时,求证:EH与FG共面;并求出此时EH与FG的交点P到直线 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.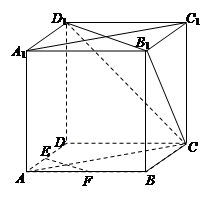
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com