
分析 由已知利用大边对大角,余弦定理可得$\frac{{a}^{2}-2a-3}{2a(a+1)}$<0,解不等式组可得:-1<a<3,利用三角形两边之和大于第三边可解得:a>1,即可得解.
解答 解:∵钝角三角形三边长为a,a+1,a+2,
∴a+2对的角为钝角,设为α,
∴cosα=$\frac{{a}^{2}+(a+1)^{2}-(a+2)^{2}}{2a(a+1)}$=$\frac{{a}^{2}-2a-3}{2a(a+1)}$<0,
解得:-1<a<3,
由a+a+1>a+2,解得:a>1,
则a的取值范围为(1,3).
故答案为:(1,3)
点评 本题主要考查了大边对大角,余弦定理,不等式组的解法,三角形两边之和大于第三边等知识在解三角形中的综合应用,考查了转化思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
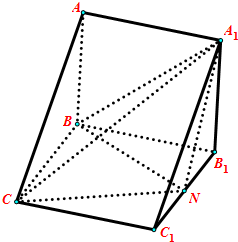 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=$\frac{1}{x-1}$ | C. | y=log2$\frac{1}{x}$ | D. | y=-tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com