
分析 (1)运用向量的数量积的坐标表示,结合两角和的正弦公式,即可求得角B的值;
(2)结合余弦定理得到△ABC为等边三角形,问题得以解决.
解答 解:(1)$\overrightarrow m$=(-2a+c,b),$\overrightarrow n$=(cosB,cosC),且 $\overrightarrow m$•$\overrightarrow n$=0.
∴(-2a+c)cosB+bcosC=0,
∴(-2sinA+sinC)cosB+sinBcosC=0,
∴-2sinAcosB+sinCcosB+sinBcosC=0,
∴-2sinAcosB+sin(C+B)=0,
∴-2sinAcosB+sinA=0,
∴cosB=$\frac{1}{2}$,
∴B=60°,
(2)由余弦定理可得b2=a2+c2-2accosB=ac,
∴(a-c)2=0,
∴a=c,
又B=60°,
∴△ABC为等边三角形,
∴A=C=60°,
∴$\frac{1}{tanA}+\frac{1}{tanC}$=$\frac{1}{\sqrt{3}}$+$\frac{1}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$
点评 本题考查向量的数量积的坐标表示,以及三角函数的化简和求值,考查正弦定理的运用,以及运算求解能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
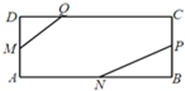 如图在长方形ABCD中,已知AB=4,BC=2,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 $\overrightarrow{MQ}$•$\overrightarrow{NP}$的值.
如图在长方形ABCD中,已知AB=4,BC=2,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 $\overrightarrow{MQ}$•$\overrightarrow{NP}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
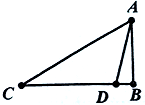 为了测量灯塔AB的高度,第一次在C点处测得∠ACB=30°,然后向前走了20米到达点D处测得∠ADB=75°,点C,D,B在同一直线上,则灯塔AB的高度为$5(\sqrt{3}+1)$.
为了测量灯塔AB的高度,第一次在C点处测得∠ACB=30°,然后向前走了20米到达点D处测得∠ADB=75°,点C,D,B在同一直线上,则灯塔AB的高度为$5(\sqrt{3}+1)$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | … | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | … | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15° | B. | 75° | C. | 105° | D. | 165° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com