
(2008•嘉定区一模)连接球面上任意两点的线段称为球的弦,已知半径为5的球上有两条长分别为6和8的弦,则此两弦中点距离的最大值是 .
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:选择题
设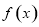 是定义在
是定义在 上恒不为零的函数,且对任意的实数
上恒不为零的函数,且对任意的实数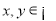 ,都有
,都有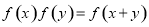 ,若
,若 ,
, ,则数列
,则数列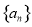 的前
的前 项和
项和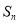 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:填空题
底面直径为10的圆柱被与底面成60°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ,离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:选择题
工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )

A.一段圆弧 B.一段抛物线 C.一段双曲线 D.一段正弦曲线
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,若OM=ON=3,则两圆圆心的距离MN= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2008•崇文区二模)若半径为1的球与120°的二面角的两个半平面切于M、N两点,则两切点间的球面距离是( ).
A.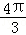 B.π C.
B.π C.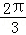 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
(2009•朝阳区二模)在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
函数f1(x)=cosx﹣sinx,记f2(x)=f1′(x),f3(x)=f2′(x),…fn(x)=fn﹣1′(x),(n∈N*,n≥2),则 =( )
=( )
A.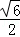 B.
B.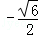 C.0 D.2008
C.0 D.2008
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com