
【题目】已知函数![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)若![]() =0,求函数
=0,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,证明
,证明![]() >0时,
>0时,![]() <
<![]()
【答案】(1)见解析;(2)见解析
【解析】
(1)求得![]() 的导数,讨论
的导数,讨论![]() ,
,![]() ,
,![]() ,解不等式可得所求单调区间;
,解不等式可得所求单调区间;
(2)分别求得![]() 的最大值,
的最大值,![]() 的最小值,比较即可得证.
的最小值,比较即可得证.
(1)若![]() ,则
,则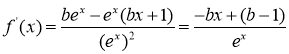 ,
,
(i)当![]() 时,
时,![]() ,函数
,函数![]() 在R上单调递减;
在R上单调递减;
(ii)当![]() 时,
时,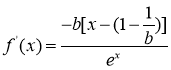 ,
,
①若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减.
单调递减.
②若![]() ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
综上可知,
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为R,无单调递增区间;
的单调递减区间为R,无单调递增区间;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)若![]() 则
则![]() ,
,![]() ,
,
要证不等式![]() ,即证
,即证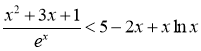 ,
,
记![]() ,则
,则![]() ,
,
故当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以![]() ;
;
又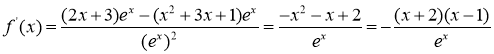 ,
,
故![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
所以![]() 时,
时,![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).设
).设![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,则“存在常数
,则“存在常数![]() ,对任意的
,对任意的![]() ,且
,且![]() ,都有
,都有![]() ”是“数列
”是“数列![]() 为等差数列”的( )
为等差数列”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月22日,依照中国文联及中国民间文艺家协会命名中国观音文化之乡的有关规定,中国文联、中国民协正式命名四川省遂宁市为“中国观音文化之乡”.
下表为2014年至2018年观音文化故里某土特产企业的线下销售额(单位:万元)
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
线下销售额 | 90 | 170 | 210 | 280 | 340 |
为了解“祝福观音、永保平安”活动的支持度.某新闻调查组对40位老年市民和40位年轻市民进行了问卷调查(每位市民从“很支持”和“支持”中任选一种),其中很支持的老年市民有30人,支持的年轻市民有15人.
(1)从以上5年中任选2年,求其销售额均超过200万元的概率;
(2)请根据以上信息列出列联表,并判断能否有85%的把握认为支持程度与年龄有关.
附:![]() ,其中
,其中![]()
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学将收集到的六组数据制作成散点图如图所示,并得到其回归直线的方程为![]() ,计算其相关系数为
,计算其相关系数为![]() ,相关指数为
,相关指数为![]() .经过分析确定点F为“离群点”,把它去掉后,再利用剩下的5组数据计算得到回归直线的方程为
.经过分析确定点F为“离群点”,把它去掉后,再利用剩下的5组数据计算得到回归直线的方程为![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() .以下结论中,不正确的是( )
.以下结论中,不正确的是( )

A.![]() >
>![]() B.
B.![]() >0,
>0,![]() >0C.
>0C.![]() =0.12D.0<
=0.12D.0<![]() <0.68
<0.68
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com