练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，曲线的参数方程是（为参数），以该直角坐标系的原点为极点， 轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）写出曲线的普通方程和直线的直角坐标方程；

    （2）设点，直线与曲线相交于两点，且，求实数的值.

    【答案】（1）曲线的普通方程为，直线的直角坐标方程为；（2）或或.

    【解析】试题分析：（1）写普通方程，则只需消去参数和根据极坐标变换公式即可轻松求得故曲线的普通方程为.直线的直角坐标方程为.（2）由题可知,所以联立和得

    ，代入韦达定理即得答案

    解析：

    （1），

    故曲线的普通方程为.

    直线的直角坐标方程为.

    （2）直线的参数方程可以写为（为参数）.

    设两点对应的参数分别为，将直线的参数方程代入曲线的普通方程可以得到 ，

    所以 或，

    解得或或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）设函数f（x）=|x﹣ |+|x﹣a|，x∈R，若关于x的不等式f（x）≥a在R上恒成立，求实数a的最大值；
    （2）已知正数x，y，z满足x+2y+3z=1，求 + + 的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a、b、c，且满足3asinC=4ccosA， =3．
    （1）求△ABC的面积S；
    （2）若c=1，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，AC为⊙O的直径，D为 的中点，E为BC的中点．

    （1）求证：DE∥AB；
    （2）求证：ACBC=2ADCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司订购了一批树苗，为了检测这批树苗是否合格，从中随机抽测 株树苗的高度，经数据处理得到如图的频率分布直方图，起中最高的 株树苗高度的茎叶图如图所示，以这 株树苗的高度的频率估计整批树苗高度的概率.

    （1）求这批树苗的高度高于 米的概率，并求图19-1中， ， ， 的值；

    （2）若从这批树苗中随机选取 株，记 为高度在 的树苗数列，求 的分布列和数学期望.

    （3）若变量 满足且 ，则称变量 满足近似于正态分布 的概率分布.如果这批树苗的高度满足近似于正态分布 的概率分布，则认为这批树苗是合格的，将顺利获得签收；否则，公司将拒绝签收.试问，该批树苗能否被签收？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正三棱柱中，为的中点.

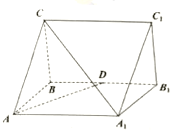
    （1）求证：；

    （2）若点为四边形内部及其边界上的点，且三棱锥的体积为三棱柱体积的，试在图中画出点的轨迹，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x+a|+|x﹣2|
    （1）当a=﹣3时，求不等式f（x）≥3的解集；
    （2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数）；以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）求曲线的普通方程与曲线的直角坐标方程；

    （Ⅱ）若把曲线各点的横坐标伸长到原来的倍，纵坐标变为原来的，得到曲线，求曲线的方程；

    （Ⅲ）设为曲线上的动点，求点到曲线上点的距离的最小值，并求此时点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f(x)对任意的m，n∈R都有f(m＋n)＝f(m)＋f(n)－1，并且x＞0时，恒有f(x)＞1.

    (1)求证：f(x)在R上是增函数；

    (2)若f(3)＝4，解不等式f(a2＋a－5)＜2

    查看答案和解析>>

    同步练习册答案