练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．若函数f（x）=$\frac{\sqrt{{x}^{2}-（a+1）x+1}}{{x}^{2}-x+1}$定义域为R，则实数a的取值范围为（　　）
    A．[-3，-1]B．[-1，3]C．[1，3]D．[-3，1]

    分析 问题转化为x2-（a+1）x+1≥0在R恒成立，根据二次函数的性质得到关于a的不等式，解出即可．

    解答 解：若函数f（x）=$\frac{\sqrt{{x}^{2}-（a+1）x+1}}{{x}^{2}-x+1}$定义域为R，
    则x2-（a+1）x+1≥0在R恒成立，
    ∴△=[-（a+1）]2-4≤0，解得：-3≤a≤1，
    故选：D．

    点评 本题考查了求函数的定义域问题，考查二次函数的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．某地拟建造一座体育馆，其设计方案侧面的外轮廓线如图所示：曲线AB是以点E的圆心的圆的一部分，其中E（0，t）（0＜t≤25），GF是圆的切线，且GF⊥AD，曲线BC是抛物线y=-ax2+50（a＞0）的一部分，CD⊥AD，且CD恰好等于圆E的半径．
    （1）若CD=30米，AD=24$\sqrt{5}$米，求t与a的值；
    （2）若体育馆侧面的最大宽度DF不超过75米，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{8}$=1的长轴长是（　　）
    A．2B．2$\sqrt{2}$C．4D．4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ex-ax-1，（a为实数），g（x）=lnx-x
    （1）讨论函数f（x）的单调区间；
    （2）求函数g（x）的极值；
    （3）求证：lnx＜x＜ex（x＞0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

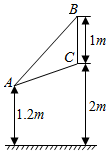    19．如图，化工厂的主控制表盘高BC=1米，表盘底边距地面2米，设值班人员坐在椅子上时，眼睛距地面1.2米，问值班人员坐在什么位置上看表盘效果最佳？（即视角∠BAC最大）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知x＞0，y＞0且满足$\frac{9x}{y}$+$\frac{4y}{x}$≥a2+a恒成立，则实数a的取值范围是[-4，3]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

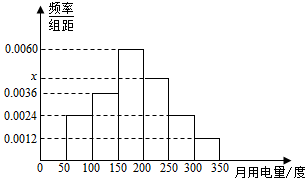    16．从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示，在这些用户中，用电量落在区间[150，250）内的户数为52．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．在某海洋军事演习编队中，指挥舰00号与驱逐舰01号、02号的距离一直保持100海里的距离，当驱逐舰01号在指挥舰00号的北偏东15°，02号在00号南偏东45°时，则驱逐舰01号与02号相距（　　）
    A．100海里B．100$\sqrt{2}$海里C．100$\sqrt{3}$海里D．200海里

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．圆心C（2，1），半径为3的圆的参数方程是（　　）
    A．$\left\{\begin{array}{l}x=2+3cosθ\\ y=1+3sinθ\end{array}\right.（θ为参数）$B．$\left\{\begin{array}{l}x=-2+3cosθ\\ y=-1+3sinθ\end{array}\right.（θ为参数）$
    C．$\left\{\begin{array}{l}x=2-3cosθ\\ y=1-3sinθ\end{array}\right.（θ为常数）$D．$\left\{\begin{array}{l}x=-2-3cosθ\\ y=-1-3sinθ\end{array}\right.（θ为参数）$

    查看答案和解析>>

    同步练习册答案