
| A�� | -6 | B�� | 6 | C�� | $\frac{3}{2}$ | D�� | -$\frac{3}{2}$ |
���� ���������ߵ������ʾ�õ�m=2x-y������Լ�������������������ν�����m��ֵ��
��� 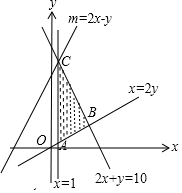 �⣺�������⣬����$\overrightarrow{a}$=��y-2x��m����$\overrightarrow{b}$=��1��-1����
�⣺�������⣬����$\overrightarrow{a}$=��y-2x��m����$\overrightarrow{b}$=��1��-1����
��$\overrightarrow{a}$��$\overrightarrow{b}$����-1����y-2x��-1��m=0��
��m=2x-y��
��x��y����Լ������$\left\{\begin{array}{l}{x��1}\\{y��\frac{1}{2}x}\\{2x+y��10}\end{array}\right.$�������������ͼ��
��m=2x-y����y=2x-m��
�൱ֱ��y=2x-m��y���ϵĽؾ����ʱ��m��С��
����ֱ��y=2x-m����C��1��8��ʱ��m����СֵΪ2��1-8=-6��
��ѡ��A��
���� ���⿼���˼����Թ滮���漰�������ߵ������ʾ���ؼ��Ƿ����õ�m��x��y�Ĺ�ϵ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��e�� | B�� | ��-�ޣ�e�� | C�� | ��1��+�ޣ� | D�� | ��-�ޣ�1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | 5 | C�� | 2$\sqrt{6}$ | D�� | 25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2��$\sqrt{3}$��-$\sqrt{3}$} | B�� | {2��$\sqrt{3}$} | C�� | {2��-$\sqrt{3}$} | D�� | {2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��2] | B�� | [-3��2] | C�� | ��-3��2�� | D�� | ��-�ޣ�-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�������ⳤ��Ϊ2��ֱ������ABCD-A��B��C��D���У�B��D���е�ΪE�䣮
��ͼ�������ⳤ��Ϊ2��ֱ������ABCD-A��B��C��D���У�B��D���е�ΪE�䣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com