Question

5．若三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC，SA=3$\sqrt{2}$，AB=1，$AC=\sqrt{2}$，∠BAC=45°，则球O的表面积为20π．

Answer 1

分析 由三棱锥S-ABC的所有顶点都在球O的球面上，AB=1，$AC=\sqrt{2}$，∠BAC=45°，知BC，∠ABC=90°，可得△ABC截球O所得的圆O′的半径，利用SA⊥平面ABC，SA=3$\sqrt{2}$，此能求出球O的半径，从而能求出球O的表面积．

解答 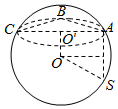解：如图，三棱锥S-ABC的所有顶点都在球O的球面上，
∵AB=1，$AC=\sqrt{2}$，∠BAC=45°
∴BC=$\sqrt{1+2-2×1×\sqrt{2}×\frac{\sqrt{2}}{2}}$=1，
∴∠ABC=90°．
∴△ABC截球O所得的圆O′的半径r=$\frac{1}{2}•\frac{1}{sin45°}$=$\frac{\sqrt{2}}{2}$，
设OO′=d，球O的半径R，则
∵SA⊥平面ABC，SA=3$\sqrt{2}$，
∴R²=$\frac{1}{2}$+d²=$\frac{1}{2}$+（3$\sqrt{2}$-d）²，
∴球O的半径R=$\sqrt{5}$，
∴球O的表面积S=4πR²=20π．
故答案为：20π．

点评 本题考查球的表面积的求法，合理地作出图形，数形结合求出球半径，是解题的关键．