
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点的极坐标;
的交点的极坐标;
(2)设![]() 是
是![]() 的一条直径,且
的一条直径,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 交
交![]() 于
于![]() 两点,直线
两点,直线![]() 交
交![]() 于
于![]() 两点,求四边形
两点,求四边形![]() 的面积的最小值.
的面积的最小值.
科目:高中数学 来源: 题型:
【题目】一饮料店制作了一款新饮料,为了进行合理定价先进行试销售,其单价![]() (元)与销量
(元)与销量![]() (杯)的相关数据如下表:
(杯)的相关数据如下表:
单价 | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量 | 120 | 110 | 90 | 70 | 60 |
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该款新饮料每杯的成本为8元,试销售结束后,请利用(1)所求的线性回归方程确定单价定为多少元时,销售的利润最大?(结果四舍五入保留到整数)
附:线性回归方程![]() 中斜率和截距最小二乗法估计计算公式:
中斜率和截距最小二乗法估计计算公式: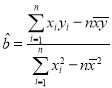 ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎期间某商场开通三种平台销售商品,收集一月内的数据如图1;为了解消费者对各平台销售方式的满意程度,该商场用分层抽样的方法抽取4%的顾客进行满意度调查,得到的数据如图2.下列说法错误的是( )
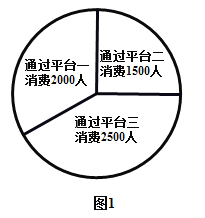
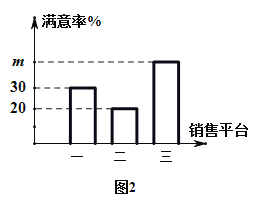
A.样本容量为240
B.若样本中对平台三满意的人数为40,则![]()
C.总体中对平台二满意的消费者人数约为300
D.样本中对平台一满意的人数为24人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是( )
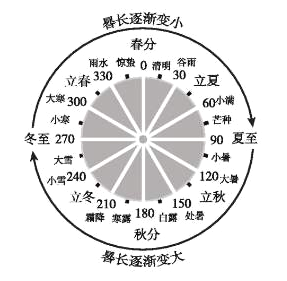
A.相邻两个节气晷长减少或增加的量为一尺
B.春分和秋分两个节气的晷长相同
C.立冬的晷长为一丈五寸
D.立春的晷长比立秋的晷长短
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如表:
送餐距离(千米) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
频数 | 15 | 25 | 25 | 20 | 15 |
以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表).
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com