
【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段![]() ,
, ![]() …
…![]() 后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
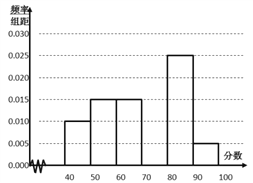
(1)求第四小组的频率,补全频率分布直方图,并估计该校学生的数学成绩的中位数.
(2)从被抽取的数学成绩是![]() 分以上(包括
分以上(包括![]() 分)的学生中选两人,求他们在同一分数段的概率.
分)的学生中选两人,求他们在同一分数段的概率.
(3)假设从全市参加高一年级期末考试的学生中,任意抽取![]() 个学生,设这四个学生中数学成绩为80分以上(包括
个学生,设这四个学生中数学成绩为80分以上(包括![]() 分)的人数为
分)的人数为![]() (以该校学生的成绩的频率估计概率),求
(以该校学生的成绩的频率估计概率),求![]() 的分布列和数学期望.
的分布列和数学期望.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】边长为2的正三角形ABC中,点D,E,G分别是边AB,AC,BC的中点,连接DE,连接AG交DE于点![]() 现将
现将![]() 沿DE折叠至
沿DE折叠至![]() 的位置,使得平面
的位置,使得平面![]() 平面BCED,连接A1G,EG.
平面BCED,连接A1G,EG.
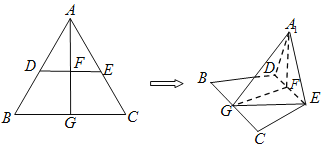
![]() 证明:DE∥平面A1BC
证明:DE∥平面A1BC
![]() 求点B到平面A1EG的距离.
求点B到平面A1EG的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
: 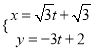 (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=x2-2mx+4在[2,+∞)上单调递增,命题q:关于x的不等式mx2+4(m-2)x+4>0的解集为R.若p∨q为真命题,p∧q为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区中央广场由两部分组成,一部分是边长为![]() 的正方形
的正方形![]() ,另一部分是以
,另一部分是以![]() 为直径的半圆,其圆心为
为直径的半圆,其圆心为![]() .规划修建的
.规划修建的![]() 条直道
条直道![]() ,
, ![]() ,
, ![]() 将广场分割为
将广场分割为![]() 个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点
个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点![]() 在半圆弧上,
在半圆弧上, ![]() 分别与
分别与![]() ,
, ![]() 相交于点
相交于点![]() ,
, ![]() .(道路宽度忽略不计)
.(道路宽度忽略不计)
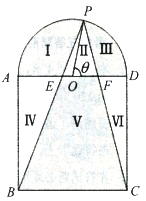
(1)若![]() 经过圆心,求点
经过圆心,求点![]() 到
到![]() 的距离;
的距离;
(2)设![]() ,
, ![]() .
.
①试用![]() 表示
表示![]() 的长度;
的长度;
②当![]() 为何值时,绿化区域面积之和最大.
为何值时,绿化区域面积之和最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com