
【题目】已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).
(1)求函数f(x)的极值;
(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求实数a的取值范围;
(3)若函数h(x)=![]() 在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
【答案】(1)见解析;(2)![]() ;(3)4
;(3)4
【解析】
(1)对![]() 求导,通过
求导,通过![]() 的正负,列表分析
的正负,列表分析![]() 的单调性进而求得极值.
的单调性进而求得极值.
(2)先求得![]() 的解析式,对其求导,原题转化为导函数
的解析式,对其求导,原题转化为导函数![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求得a的范围.(3)由题意知
,求得a的范围.(3)由题意知![]() 在
在![]() 上有两个不等实根,即
上有两个不等实根,即![]() 在
在![]() 上有两个不等实根,对
上有两个不等实根,对![]() 求导分析可得
求导分析可得![]() 在
在![]() 和
和![]() 上各有一个实根,从而得到极大值
上各有一个实根,从而得到极大值![]() ,将
,将![]() 视为关于
视为关于![]() 的函数,求导得到
的函数,求导得到![]() ,又因为
,又因为![]() ,得到整数b的最小值.
,得到整数b的最小值.
(1)![]() ,
,![]() ,令
,令![]() ,解得
,解得![]() ,列表:
,列表:
|
| 2 |
|
| + | 0 | - |
|
| 极大值 |
|
∴当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() ,无极小值
,无极小值
(2)由![]() ,得
,得![]()
![]()
∵![]() ,令
,令![]() ,
,
∴函数![]() 在区间
在区间![]() 上单调递增等价于对任意的
上单调递增等价于对任意的![]() ,函数
,函数![]() 恒成立
恒成立
∴![]() ,解得
,解得![]() .
.
(3)![]() ,
,![]()
令![]() ,
,
∵![]() 在
在![]() 上既存在极大值又存在极小值,∴
上既存在极大值又存在极小值,∴![]() 在
在![]() 上有两个不等实根,
上有两个不等实根,
即![]() 在
在![]() 上有两个不等实根
上有两个不等实根![]() .
.
∵![]()
∴当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
则![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]()
∵![]() 在
在![]() 上连续且
上连续且![]() ,
,![]()
∴![]() 在
在![]() 和
和![]() 上各有一个实根
上各有一个实根
∴函数![]() 在
在![]() 上既存在极大值又存在极小值时,有
上既存在极大值又存在极小值时,有![]() ,并且在区间
,并且在区间![]() 上存在极小值
上存在极小值![]() ,在区间
,在区间![]() 上存在极大值
上存在极大值![]() .
.
∴![]() ,且
,且![]()
![]() ,
,![]()
![]()
令![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
∵![]() ,∴
,∴![]() ,即
,即![]() ,则
,则![]()
∵![]() 的极大值小于整数
的极大值小于整数![]() ,∴满足题意的整数
,∴满足题意的整数![]() 的最小值为4.
的最小值为4.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知某公司成本为![]() 元,所得的利润
元,所得的利润![]() 元的几组数据入下.
元的几组数据入下.
第一组 | 第二组 | 第三组 | 第四组 | 第五组 | |
| 1 | 4 | 5 | 2 | 3 |
| 2 | 1 | 3 | 4 | 0 |
根据上表数据求得回归直线方程为:![]()
(1)若这个公司所规划的利润为200万元,估算一下它的成本可能是多少?(保留1位小数)
(2)在每一组数据中,![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() ;
;![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() ;
;![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() .随机抽两组进行分析,则抽到有事件
.随机抽两组进行分析,则抽到有事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人事部门对参加某次专业技术考试的100人的成绩进行了统计,绘制的频率分布直方图如图所示.规定80分以上者晋级成功,否则晋级失败(满分为100分).
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |

参考公式:![]() ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化环境,某公园欲将一块空地规划建成休闲草坪,休闲草坪的形状为如图所示的四边形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=
百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).

(1)当cos![]() =
=![]() 时,求小路AC的长度;
时,求小路AC的长度;
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A. 22种 B. 24种 C. 25种 D. 27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
(3)队长中至少有1人参加;
(4)既要有队长,又要有女运动员.
查看答案和解析>>
科目:高中数学 来源: 题型:
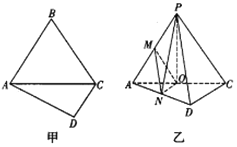
【题目】如图所示甲,在四边形ABCD中,![]() ,
,![]() ,
,![]() 是边长为8的正三角形,把
是边长为8的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
![]() 求证:
求证:![]() 平面PON;
平面PON;
![]() 求三棱锥
求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com