
【题目】已知某公司成本为![]() 元,所得的利润
元,所得的利润![]() 元的几组数据入下.
元的几组数据入下.
第一组 | 第二组 | 第三组 | 第四组 | 第五组 | |
| 1 | 4 | 5 | 2 | 3 |
| 2 | 1 | 3 | 4 | 0 |
根据上表数据求得回归直线方程为:![]()
(1)若这个公司所规划的利润为200万元,估算一下它的成本可能是多少?(保留1位小数)
(2)在每一组数据中,![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() ;
;![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() ;
;![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() .随机抽两组进行分析,则抽到有事件
.随机抽两组进行分析,则抽到有事件![]() 发生的概率.
发生的概率.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点在
的两焦点在![]() 轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为
轴上,且短轴的两个顶点与其中一个焦点的连线构成斜边为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆的方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以线段
,使得以线段![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设锐角![]() 的外接圆的半径为
的外接圆的半径为![]() ,在
,在![]() 内取外接圆的同心圆
内取外接圆的同心圆![]() ,其半径为
,其半径为![]()
![]() ,从圆
,从圆![]() 上任取一点
上任取一点![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
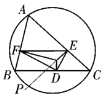
(1)求证:![]() 的面积为定值;
的面积为定值;
(2)猜想:当![]() 为任意三角形、同心圆
为任意三角形、同心圆![]() 为任意同心圆时,结论是否成立(不要求证明)?
为任意同心圆时,结论是否成立(不要求证明)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙两个学生在高二的6次数学测试的成绩(百分制)制成如图所示的茎叶图,进入高三后,由于改进了学习方法,甲、乙这两个学生的考试成绩预计同时有了大的提升:若甲(乙)的高二任意一次考试成绩为![]() ,则甲(乙)的高三对应的考试成绩预计为
,则甲(乙)的高三对应的考试成绩预计为![]() .
.

(1)试预测:高三6次测试后,甲、乙两个学生的平均成绩分别为多少?谁的成绩更稳定?
(2)若已知甲、乙两个学生的高二6次考试成绩分别由低到高进步的,定义![]() 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求
为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,PA⊥平面ABC,∠ABC=90°,AB=PA=6,BC=8,则( )
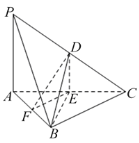
A.三棱锥D-BEF的体积为6
B.直线PB与直线DF垂直
C.平面DEF截三棱锥P-ABC所得的截面面积为12
D.点P与点A到平面BDE的距离相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).
(1)求函数f(x)的极值;
(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求实数a的取值范围;
(3)若函数h(x)=![]() 在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com