
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,点M在线段PC上,且PM=2MC,N为AD的中点. 
(1)求证:平面PAD⊥平面PNB;
(2)若平面PAD⊥平面ABCD,求三棱锥P﹣NBM的体积.
【答案】
(1)证明:∵PA=PD,N为AD的中点,∴PN⊥AD,
∵底面ABCD为菱形,∠BAD=60°,∴PA=AB,AN=AN,∠PAN=∠BAN,
∴△PNA≌△BNA,则BN⊥AD,
∵PN∩BN=N,∴AD⊥平面PNB,
又AD平面PAD,∴平面PAD⊥平面PNB
(2)解:∵PA=PD=AD=2,∴PN=NB= ![]() ,
,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PN⊥AD,
∴PN⊥平面ABCD,∴PN⊥BN,
∴S△PNB= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
∵AD⊥平面PNB,AD∥BC,∴BC⊥平面PNB,
∵PM=2MC,∴VP﹣NBM=VM﹣PNB= ![]() VC﹣PNB=
VC﹣PNB= ![]() ×
× ![]() ×
× ![]() ×2=
×2= ![]() .
.
【解析】(1)由题意证明△PNA≌△BNA,得到BN⊥AD,再由线面垂直的判定证得AD⊥平面PNB,最后由面面垂直的判定得答案;(2)由面面垂直的性质得到PN⊥平面ABCD,进一步得到PN⊥BN,再由等积法把三棱锥P﹣NBM的体积转化为棱锥C﹣PNB的体积求解.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,若
,若![]() 为等腰直角三角形,且直线
为等腰直角三角形,且直线![]() 被圆
被圆![]() 所截得的弦长为2.
所截得的弦长为2.
(1)求椭圆的方程;
(2)直线![]() :
:![]() 与椭圆交于点
与椭圆交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 与椭圆交于点
与椭圆交于点![]() ,点
,点![]() 为
为![]() 的重心,求证:
的重心,求证:![]() 的面积
的面积![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”; 丁说:“
两项作品未获得一等奖”; 丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学只有两位说的话是对的,则获得一等奖的作品是( )
A. ![]() 作品 B.
作品 B. ![]() 作品 C.
作品 C. ![]() 作品 D.
作品 D. ![]() 作品
作品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若a,b,c∈R,f(a),f(b),f(c)为某一个三角形的边长,则实数m的取值范围是( )
,若a,b,c∈R,f(a),f(b),f(c)为某一个三角形的边长,则实数m的取值范围是( )
A.[ ![]() ,1]
,1]
B.[0,1]
C.[1,2]
D.[ ![]() ,2]
,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校团委会组织某班以小组为单位利用周末时间进行一次社会实践活动,每个小组有5名同学,在活动结束后,学校团委会对该班的所有同学进行了测试,该班的A,B两个小组所有同学得分(百分制)的茎叶图如图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组同学的平均分高一分.
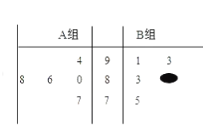
(1)若在B组学生中随机挑选1人,求其得分超过86分的概率;
(2)现从A、B两组学生中分别随机抽取1名同学,设其分数分别为m、n,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com