练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知A、B、C、D为圆O上的四点，直线DE为圆O的切线，AC∥DE，AC与BD相交于H点
    （Ⅰ）求证：BD平分∠ABC
    （Ⅱ）若AB=4，AD=6，BD=8，求AH的长．
    （Ⅰ）∵AC∥DE，直线DE为圆O的切线，∴D是弧
    AC
    的中点，即
    AD
    =
    DC

    又∠ABD，∠DBC与分别是两弧
    AD
    ，
    DC
    所对的圆周角，故有∠ABD=∠DBC，
    所以BD平分∠ABC
    （Ⅱ）∵由图∠CAB=∠CDB且∠ABD=∠DBC
    ∴△ABH∽△DBC，∴
    AH
    CD
    =
    AB
    BD

    又
    AD
    =
    DC

    ∴AD=DC，
    ∴
    AH
    AD
    =
    AB
    BD

    ∵AB=4，AD=6，BD=8
    ∴AH=3
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BBl∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．
    （1）当t为何值时，AD=AB，并求出此时DE的长度；
    （2）当△DEG与△ACB相似时，求t的值；
    （3）以DH所在直线为对称轴，线段AC经轴对称变换后的图形为A′C′．
    ①当t＞
    3
    5
    时，连接C′C，设四边形ACC′A′的面积为S，求S关于t的函数关系式；
    ②当线段A′C′与射线BB，有公共点时，求t的取值范围（写出答案即可）．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，AB为⊙O的直径，弦AC、BD交于点P，若AB=3，CD=1，则sin∠APD的值为（　　）
    A．
    1
    3
    		B．
    		2
    3
    		C．
    2
    3
    		D．
    2
    		2
    3

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    ⊙O的两条弦AB、CD相交于点P，已知AP=2cm，BP=6cm，CP：PD=1：3，则CD=______．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，PC与圆O相切于点C，直线PO交圆O于A，B两点，弦CD垂直AB于E．则下面结论中，错误的结论是（　　）
    A．△BEC∽△DEAB．∠ACE=∠ACPC．DE2=OE•EPD．PC2=PA•AB

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，已知圆O1与圆O2外切于点P，直线AB是两圆的外公切线，分别与两圆相切于A、B两点，AC是圆O1的直径，过C作圆O2的切线，切点为D．
    （Ⅰ）求证：C，P，B三点共线；
    （Ⅱ）求证：CD=CA．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    采用系统抽样方法从人中抽取人做问卷调查，为此将他们随机编号为,，……，，分组后在第一组采用简单随机抽样的方法抽到的号码为．抽到的人中，编号落入区间的人做问卷，编号落入区间的人做问卷，其余的人做问卷．则抽到的人中，做问卷的人数为 （ ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    [2012·四川高考]交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43，则这四个社区驾驶员的总人数N为(　　)
    A．101B．808C．1212D．2012

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本试卷共40分，考试时间30分钟）
    21．（选做题）本大题包括A，B，C，D共4小题，请从这4题中选做2小题． 每小题10分，共20分．请在答题卡上准确填涂题目标记． 解答时应写出文字说明、证明过程或演算步骤．
    A． 选修4－1：几何证明选讲
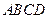    如图，是边长为的正方形，以为圆心，为半径的圆弧与以为直径的半⊙O交于点，延长交于．
    （1）求证：是的中点；（2）求线段的长．

    查看答案和解析>>

    同步练习册答案