
| A. | 6时 | B. | 7时 | C. | 8时 | D. | 9时 |
分析 求导并化简y′=-$\frac{3}{8}$t2-$\frac{3}{2}$t+36=-$\frac{3}{8}$(t-8)(t+12),从而确定函数的单调性及最值点即可.
解答 解:∵y=-$\frac{1}{8}$t3-$\frac{3}{4}$t2+36t-$\frac{629}{4}$,
∴y′=-$\frac{3}{8}$t2-$\frac{3}{2}$t+36
=-$\frac{3}{8}$(t2+4t-12×8)
=-$\frac{3}{8}$(t-8)(t+12),
故函数y=-$\frac{1}{8}$t3-$\frac{3}{4}$t2+36t-$\frac{629}{4}$在(0,8)上是增函数,
在(8,24)上减函数;
故当t=8时,y有最大值,
故通过路段用时最多的时刻是8时,
故选C.
点评 本题考查了导数的综合应用及函数的单调性与最值的判断与求法.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2017×22015 | B. | 2017×22014 | C. | 2016×22015 | D. | 2016×22014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
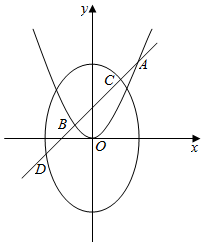 如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.
如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
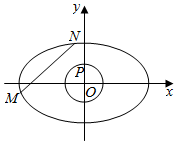 如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.
如图,已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,圆O:x2+y2=1,其中M,N是椭圆C上的两个动点,P是圆O上一个动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com