
分析 分别根据三角函数公式和性质进行判断即可得到结论.
解答 解:①∵sinα+cosα=$\sqrt{2}$sin($α+\frac{π}{4}$),
∴当α∈(0,$\frac{π}{2}$),$α+\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),
∴$\sqrt{2}$sin($α+\frac{π}{4}$)∈(1,2],
∴不存在α∈(0,$\frac{π}{2}$),使sinα+cosα=$\frac{1}{3}$;故①错误;
②若y=cosx为减函数,则2kπ≤x≤2kπ+π,k∈Z,
当2kπ≤x≤2kπ+π,k∈Z时,sinx≥0,
即不存在区间(a,b),使y=cosx为减函数且sinx<0;故②错误;
③当x=-$\frac{π}{6}$时,y=4sin(-$\frac{π}{6}$×2+$\frac{π}{3}$)=4sin0=0,
则函数y=4sin(2x+$\frac{π}{3}$)的图象关于点(-$\frac{π}{6}$,0)对称;故③正确,
④函数y=cos2x+sin($\frac{π}{2}$-x)=cos2x+cosx,则函数为偶函数,
又y=cos2x+cosx=2cos2x+cosx-1=2(cosx+$\frac{1}{4}$)2-$\frac{9}{8}$,
∵-1≤cosx≤1,
∴当cosx=1时,函数取得最大值,当cosx=-$\frac{1}{4}$时,函数取得最小值,故函数既有最大值,又有最小值.故④正确,
故正确的是③④,
故答案为:③④
点评 本题主要考查与三角函数有关的命题的真假判断,要求熟练掌握三角函数的公式和性质.考查学生的推理判断能力.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
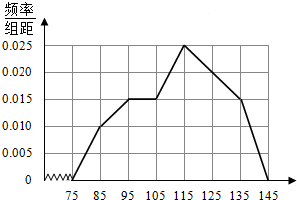 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{0}$ | B. | $\overrightarrow{PC}$+$\overrightarrow{PA}$=$\overrightarrow{0}$ | C. | $\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ | D. | $\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com