
【题目】在极坐标系中,射线![]() 与圆
与圆![]() 交于点
交于点![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴正半轴建立平面直角坐标系
轴正半轴建立平面直角坐标系![]()
(1)求点![]() 的直角坐标和椭圆
的直角坐标和椭圆![]() 的参数方程;
的参数方程;
(2)若![]() 为椭圆
为椭圆![]() 的下顶点,
的下顶点,![]() 为椭圆
为椭圆![]() 上任意一点,求
上任意一点,求![]() 的取值范围
的取值范围
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】若数列{an}满足:对任意n∈N*,均有an=bn+cn成立,且{bn},{cn}都是等比数列,则称(bn,cn)是数列{an}的一个等比拆分.
(1)若an=2n,且(bn,bn+1)是数列{an}的一个等比拆分,求{bn}的通项公式;
(2)设(bn,cn)是数列{an}的一个等比拆分,且记{bn},{cn}的公比分别为q1,q2;
①若{an}是公比为q的等比数列,求证:q1=q2=q;
②若a1=1,a2=2,q1q2=﹣1,且对任意n∈N*,an+13<anan+1an+2+an+2﹣an恒成立,求a3的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且a1+a3=30,2S2是3S1和S3的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足![]() ,求数列{bn}前n项和Tn.
,求数列{bn}前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
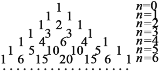
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中曲线
中曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程以及直线
的普通方程以及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)将曲线![]() 向左平移2个单位,再将曲线
向左平移2个单位,再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .直线
.直线![]() 与
与![]() 轴正半轴和
轴正半轴和![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与椭圆分别交于点
,与椭圆分别交于点![]() 、
、![]() ,各点均不重合且满足
,各点均不重合且满足![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)若![]() ,试证明:直线
,试证明:直线![]() 过定点并求此定点.
过定点并求此定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解本市![]() 万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布
万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,发现其成绩服从正态分布![]() ,现从某校随机抽取了
,现从某校随机抽取了![]() 名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.

(1)估算该校![]() 名学生成绩的平均值
名学生成绩的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)求这![]() 名学生成绩在
名学生成绩在![]() 内的人数;
内的人数;
(3)现从该校![]() 名考生成绩在
名考生成绩在![]() 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:若![]() ,则
,则![]() ,
, ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com