
在锐角 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
.
(1)求B;
(2)若 ,求
,求 .
.
(1) ;(2)4.
;(2)4.
解析试题分析:(1)首先用诱导公式把 化成
化成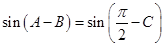 ,
,
因为 都是锐角,根据正弦函数的单调性知:
都是锐角,根据正弦函数的单调性知: ,再结合三角形内角和定理可解角
,再结合三角形内角和定理可解角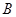 .
.
(2)由(1)的结果,在 中,已知两边和其中一边的对角,可用正弦定理或余弦定理求
中,已知两边和其中一边的对角,可用正弦定理或余弦定理求 .要注意锐角三角形条件,防止增解.
.要注意锐角三角形条件,防止增解.
试题解析:(1)由sin(A-B)=cosC,得sin(A-B)=sin( -C).
-C).
∵△ABC是锐角三角形,
∴A-B= -C,即A-B+C=
-C,即A-B+C= , ①
, ①
又A+B+C=π, ②
由②-①,得B= . 6分
. 6分
(2)由余弦定理b2=c2+a2-2cacosB,得
(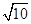 )2=c2+(3
)2=c2+(3 )2-2c×3
)2-2c×3 cos
cos ,
,
即c2-6c+8=0,解得c=2,或c=4.
当c=2时,b2+c2-a2=(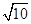 )2+22-(3
)2+22-(3 )2=-4<0,
)2=-4<0,
∴b2+c2<a2,此时A为钝角,与已知矛盾,∴c≠2.
故c=4. 12分
考点:1、诱导公式;2、正弦定理、余弦定理、解三角形.


科目:高中数学 来源: 题型:解答题
已知△ABC的内角A,B,C所对的边分别是a,b,c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,C= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,已知角A= , sin B=3sin C.
, sin B=3sin C.
(1)求tan C的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com