
分析 由题意和偶函数的性质判断出函数f(x)的对称性,由图象平移、f(x+1)的单调性、f(x)法对称性判断出f(x)的单调性,结合条件画出f(x)的图象,根据函数的单调性和图象,求出不等式(x-1)f(x)≤0的解集.
解答 解:∵函数y=f(x+1)是定义在(-∞,0)∪(0,+∞)上的偶函数,
∴f(x+1)=f(-x+1),则f(x)的图象关于直线x=1对称,
∵函数y=f(x+1)在(-∞,0)上是减函数,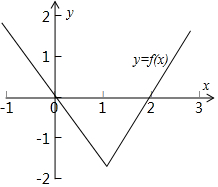
∴函数f(x)在(-∞,1)上是减函数,
在(1,+∞)上是增函数,
则由f(2)=0得f(0)=0,如图所示:
∴当x>1时,f(x)≤0=f(2),解得1<x≤2
当x<1时,f(x)≥0=f(0),得x≤0,即x≤0,
同时,当x=1时,(x-1)f(x)≤0也成立;
综上,等式(x-1)f(x)≤0的解集是(-∞,0]∪[1,2],
故答案为:(-∞,0]∪[1,2].
点评 本题考查函数的单调性、奇偶性、对称性的应用,函数图象的平移,以及根据函数的单调性把不等式转化为自变量不等式,考查转化思想、数形结合思想、分类讨论思想,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
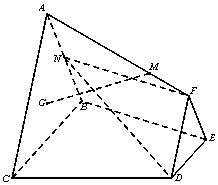 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),查看答案和解析>>
科目:高中数学 来源: 题型:填空题
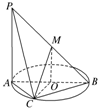 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com