
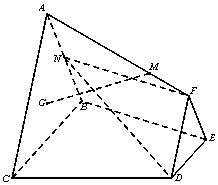
 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),分析 (Ⅰ)当λ=$\frac{2}{3}$时,连AG延长交BC于P,证明GM∥PF,P,D,F,N四点共面,即可证明:GM∥平面DFN
(Ⅱ)若直线MN与CD所成角为$\frac{π}{3}$,以P为原点,PC为x轴,PE为y轴,PA为z轴建立空间直角坐标系,利用向量的夹角公式求二面角M-BC-D的余弦值.
解答 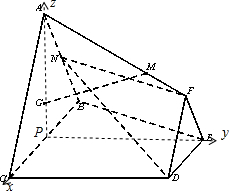 (Ⅰ)证明:连AG延长交BC于P,
(Ⅰ)证明:连AG延长交BC于P,
因为点G为△ABC的重心,所以$\frac{AG}{AP}$=$\frac{2}{3}$--------------------(1分)
又$\overrightarrow{AM}$=λ$\overrightarrow{AF}$,λ=$\frac{2}{3}$,所以$\frac{AG}{AP}$=$\frac{AM}{AF}$=$\frac{2}{3}$,所以GM∥PF;----------(2分)
因为AC∥DF,DE∥BC,所以平面ABC∥平面DEF,
又△DEF与△ABC分别是棱长为1与2的正三角形,N为AB中点,P为BC中点,所以NP∥AC,
又AC∥DF,------------(3分)
所以NP∥DF,得P,D,F,N四点共面
∴GM∥平面DFN-----------------------------------------------(5分)
(Ⅱ)平面ABC⊥平面BCDE,易得平面DEF⊥平面BCDE,
以P为原点,PC为x轴,PE为y轴,PA为z轴建立空间直角坐标系,
则C(1,0,0),D(1,1,0),A(0,0,$\sqrt{3}$),F($\frac{1}{2}$,1,$\frac{\sqrt{3}}{2}$),B(-1,0,0),N(-$\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),----(7分)
设M(x,y,z),
∵$\overrightarrow{AM}$=λ$\overrightarrow{AF}$,∴M($\frac{λ}{2}$,λ,$\sqrt{3}-\frac{\sqrt{3}}{2}λ$),$\overrightarrow{NM}$=($\frac{λ+1}{2}$,λ,$\frac{\sqrt{3}}{2}(1-λ)$),$\overrightarrow{CD}$=(0,1,0)
因为MN与CD所成角为$\frac{π}{3}$,所以$\frac{λ}{\sqrt{(\frac{λ+1}{2})^{2}+{λ}^{2}+\frac{3}{4}(1-λ)^{2}}}$=$\frac{1}{2}$,----------------(9分)
得2λ2+λ-1=0,∴λ=$\frac{1}{2}$,∴M($\frac{1}{4}$,$\frac{1}{2}$,$\frac{3\sqrt{3}}{4}$),
设平面MBC的法向量$\overrightarrow{n}$=(a,b,c),$\overline{BC}$=(2,0,0),$\overrightarrow{BM}$=($\frac{5}{4}$,$\frac{1}{2}$,$\frac{3\sqrt{3}}{4}$),
则$\left\{\begin{array}{l}{2a=0}\\{\frac{1}{2}b+\frac{3\sqrt{3}}{4}c=0}\end{array}\right.$,取$\overrightarrow{n}$=(0,3$\sqrt{3}$,-2),
面BCD的法向量$\overrightarrow{v}$=(0,0,1),所以二面角M-BC-D的余弦值=$\frac{|-2|}{\sqrt{31}}$=$\frac{2\sqrt{31}}{31}$-----------------------------(12分)
点评 本题考查线面平行的证明,考查二面角M-BC-D的余弦值,考查向量方法的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 | |
| B. | 若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误 | |
| C. | 从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病 | |
| D. | 以上三种说法都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{1+{x}^{2}}$ | B. | -$\frac{2x}{1+{x}^{2}}$ | C. | $\frac{2x}{1+{x}^{2}}$ | D. | -$\frac{x}{1+{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | $[{-\frac{2}{3},3}]$ | C. | $[{-\frac{2}{3},\frac{10}{3}}]$ | D. | $[{-1,\frac{10}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n+1 | B. | 2n-3 | C. | 2n-1 | D. | 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com