
| A. | $\frac{x}{1+{x}^{2}}$ | B. | -$\frac{2x}{1+{x}^{2}}$ | C. | $\frac{2x}{1+{x}^{2}}$ | D. | -$\frac{x}{1+{x}^{2}}$ |
分析 利用换元法,设$\frac{1-x}{1+x}=t$,则x=$\frac{1-t}{t+1}$,代入从而化简可得.
解答 解:已知f($\frac{1-x}{1+x}$)=$\frac{1-{x}^{2}}{1+{x}^{2}}$,
设$\frac{1-x}{1+x}=t$,则x=$\frac{1-t}{t+1}$,
那么:f($\frac{1-x}{1+x}$)=$\frac{1-{x}^{2}}{1+{x}^{2}}$转化为g(t)=$\frac{1-(\frac{1-t}{1+t})^{2}}{1+(\frac{1-t}{1+t})^{2}}$=$\frac{2t}{1+{t}^{2}}$,
∴f(x)的解析式可取为f(x)=$\frac{2x}{1+{x}^{2}}$,
故选C.
点评 本题考查了函数解析式的求法,利用了换元法,属于基础题.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $(6,6\sqrt{2})$或$(6,-6\sqrt{2})$ | B. | $(4,4\sqrt{3})$或$(4,-4\sqrt{3})$ | C. | (3,6)或(3,-6) | D. | $(9,6\sqrt{3})$或$(9,-6\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或-$\frac{17}{18}$ | B. | $\frac{17}{18}$ | C. | 1 | D. | $-\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
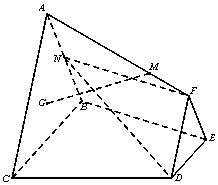 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{3π}{4}$个单位长度 | B. | 向右平移$\frac{3π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{3π}{16}$个单位长度 | D. | 向右平移$\frac{3π}{16}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com