
| A. | [-1,3] | B. | $[{-\frac{2}{3},3}]$ | C. | $[{-\frac{2}{3},\frac{10}{3}}]$ | D. | $[{-1,\frac{10}{3}}]$ |
分析 利用余弦定理求得AB、AC的值,再根据E是线段BC较靠近点C的一个四等分点,利用两个向量的加减法的法则,以及其几何意义,两个向量数量积的运算求得 $\overrightarrow{AP}$•$\overrightarrow{AE}$=$\frac{12λ-2}{3}$,λ∈[0,1],从而求得它的取值范围.
解答  解:设AB=AC=x,则由BC=4,∠BAC=120°,
解:设AB=AC=x,则由BC=4,∠BAC=120°,
利用余弦定理可得16=x2+x2-2x•xcos120°,∴x=$\sqrt{\frac{16}{3}}$.
∴$\overrightarrow{AB}•\overrightarrow{AC}$=x•x•cos120°=-$\frac{8}{3}$.
∵$\overrightarrow{BE}$=3$\overrightarrow{EC}$,∴E是线段BC较靠近点C的一个四等分点,
若P是BC边上的动点,则$\overrightarrow{BP}$=λ$\overrightarrow{BC}$,λ∈[0,1],
∴$\overrightarrow{AP}$•$\overrightarrow{AE}$=($\overrightarrow{AB}$+$\overrightarrow{BP}$)•($\overrightarrow{AB}$+$\overrightarrow{BE}$)=($\overrightarrow{AB}$+λ$\overrightarrow{BC}$)•($\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{BC}$)
=[(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AC}$]•($\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$ )
=$\frac{1-λ}{4}$•${\overrightarrow{AB}}^{2}$+($\frac{3-3λ}{4}$+$\frac{λ}{4}$)$\overrightarrow{AB}•\overrightarrow{AC}$+$\frac{3λ}{4}$${\overrightarrow{AC}}^{2}$
=$\frac{1-λ}{4}$•$\frac{16}{3}$+$\frac{3-2λ}{4}$•(-$\frac{8}{3}$)+$\frac{3λ}{4}$•$\frac{16}{3}$=$\frac{12λ-2}{3}$,
故当λ=0时,$\overrightarrow{AP}$•$\overrightarrow{AE}$ 取得最小值为-$\frac{2}{3}$,当λ=1时,$\overrightarrow{AP}$•$\overrightarrow{AE}$ 取得最大值为$\frac{10}{3}$,
故选:C.
点评 本题主要考查余弦定理,两个向量的加减法的法则,以及其几何意义,两个向量数量积的运算,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
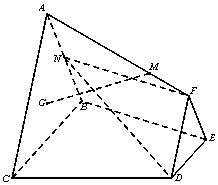 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | h(x)<g(x) | B. | h(x)>g(x) | C. | h(x)+g(a)>g(x)+h(a) | D. | h(x)+g(b)>g(x)+h(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≥x | |
| B. | 命题“若x=1,则x2=1”的逆命题 | |
| C. | ?α0,β0∈R,使得sin(α0+β0)=sinα0+sinβ0 | |
| D. | 命题“若x≠y,则sinx≠siny”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 1+lg99 | D. | 2+lg99 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com