
分析 (1)a1,a2,a5成等比数列.可得${a}_{2}^{2}$=a1a5,又a1=1,可得(1+d)2=1×(1+4d),d≠0,解得d即可得出.
(2)${b_n}=\frac{a_n}{3^n}$=$\frac{2n-1}{{3}^{n}}$,利用错位相减法、等比数列的求和公式即可得出.
解答 解:(1)∵a1,a2,a5成等比数列.∴${a}_{2}^{2}$=a1a5,又a1=1,
∴(1+d)2=1×(1+4d),d≠0,解得d=2.
∴an=2n-1.
(2)${b_n}=\frac{a_n}{3^n}$=$\frac{2n-1}{{3}^{n}}$,
∴数列{bn}的前n项和Tn=$\frac{1}{3}+\frac{3}{{3}^{2}}$+$\frac{5}{{3}^{3}}$+…+$\frac{2n-1}{{3}^{n}}$,
$\frac{1}{3}{T}_{n}$=$\frac{1}{{3}^{2}}+\frac{3}{{3}^{3}}$+…+$\frac{2n-3}{{3}^{n}}$+$\frac{2n-1}{{3}^{n+1}}$.
相减可得:$\frac{2}{3}{T}_{n}$=$\frac{1}{3}+2(\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}})$-$\frac{2n-1}{{3}^{n+1}}$=$\frac{1}{3}+2×\frac{\frac{1}{9}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$-$\frac{2n-1}{{3}^{n+1}}$.
可得:Tn=1-$\frac{n+1}{{3}^{n}}$.
点评 本题考查了错位相减法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
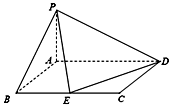 如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | 8 | C. | $\frac{{8\sqrt{5}}}{5}$ | D. | $\frac{{8\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,8) | B. | (1,+∞) | C. | (4,8) | D. | (1,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
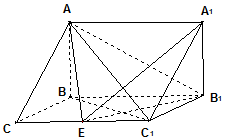 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
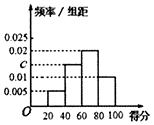 某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记为0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com