
分析 (1)直接由x的范围求得相位的范围,则函数的值域可求;
(2)化正弦为余弦,然后换元,配方后对a分类讨论求得函数的最值.
解答 解:(1)当x∈[$-\frac{π}{2}$,$\frac{π}{3}$]时,2x$-\frac{π}{6}$∈[$-\frac{7π}{6}$,$\frac{π}{2}$],
∴sin(2x$-\frac{π}{6}$)∈[-1,1],
∴$y=sin(2x-\frac{π}{6})+2,x∈[{-\frac{π}{2},\frac{π}{3}}]$的值域∈[1,3];
(2)当x∈[0,π]时,设t=cosx∈[-1,1],
∴函数y=sin2x-acosx+3=(1-cos2x)-acosx+3
=-cos2x-acosx+4=-(cosx+$\frac{a}{2}$)2+4+$\frac{{a}^{2}}{4}$=$-(t+\frac{a}{2})^{2}+4+\frac{{a}^{2}}{4}$,
由二次函数可知:
当$-\frac{a}{2}≤-1$,即a≥2时,函数取最大值3+a,最小值为3-a;
当-1$<-\frac{a}{2}≤0$,即0≤a<2时,函数取最大值$4+\frac{{a}^{2}}{4}$,取最小值3-a;
当0<$-\frac{a}{2}<1$,即-2<a<0时,函数取得最大值$4+\frac{{a}^{2}}{4}$,最小值为3+a;
当$-\frac{a}{2}≥1$,即a≤-2时,函数取得最大值3-a,最小值为3+a.
点评 本题考查三角函数的最值,考查换元法和分类讨论的数学思想方法,是中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{5}$,+∞) | B. | (-∞,$\frac{3}{5}$] | C. | (-$\frac{3}{5}$,+∞) | D. | $({-\frac{3}{5},\frac{3}{5}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
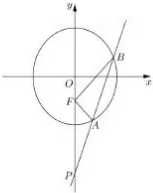 如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P
如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<1 | B. | a<2 | C. | a≤2 | D. | a≤3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com