
分析 (1)利用数列递推式,n分别取1,2,3,代入计算,即可得到结论;
(2)令Sn=a1+a2+…+an,Sn2=a13+a23+…+an3(n∈N*).可得再写一式,两式相减,可得数列{an}的任一项an与它的前一项an-1间的递推关系;利用a1=1,a2017=-2016,所以无穷数列{an}的前2016项组成首项和公差均为1的等差数列,从第2016项开始组成首项为-2016,公比为-1的等比数列,从而可得数列的通项.
(3)根据递推式得出An的所有元素规律,利用归纳法得出结论.
解答 解:(1)当n=1时,a13=a12,由a1≠0得a1=1.
当n=2时,1+a23=(1+a2)2,由a2≠0得a2=2或a2=-1.
当n=3时,1+a23+a33=(1+a2+a3)2,若a2=2得a3=3或a3=-2;若a2=-1得a3=1;
综上讨论,满足条件的数列有三个:1,2,3或1,2,-2或1,-1,1.
(2)令Sn=a1+a2+…+an,则Sn2=a13+a23+…+an3(n∈N*).
从而(Sn+an+1)2=a13+a23+…+an3+an+13,
两式相减,结合an+1≠0,得2Sn=an+12-an+1.
当n=1时,由(1)知a1=1;
当n≥2时,2an=2(Sn-Sn-1)=(an+12-an+1)-(an2-an),即(an+1+an)(an+1-an-1)=0,
所以an+1=-an或an+1=an+1.
又a1=1,a2017=-2016,所以无穷数列{an}的前2016项组成首项和公差均为1的等差数列,从第2016项开始组成首项为-2016,公比为-1的等比数列.
an=$\left\{\begin{array}{l}{n,1≤n≤2016}\\{(-1)^{n}•2016,n>2016}\end{array}\right.$.
(3)由(2)可知a1=1,an=-an-1或an=an-1+1(n≥2),
故A1={1},A2={-1,2},A3={1,-2,3},A4={-1,2,-3,4},…
∴当n为奇数时,An的所有元素之和为1+3+5+…+n-(2+4+6+…n-1)=$\frac{1+n}{2}•\frac{n+1}{2}$-$\frac{n+1}{2}•\frac{n-1}{2}$=$\frac{n+1}{2}$,
当n为偶数时,An的所有元素之和为2+4+6+…+n-(1+3+5+…+n-1)=$\frac{n+2}{2}•\frac{n}{2}$-$\frac{n}{2}•\frac{n}{2}$=$\frac{n}{2}$.
点评 本题主要考查数列通项、求和与不等式等知识,考查化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
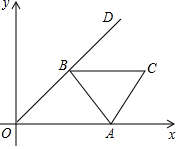 如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.
如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
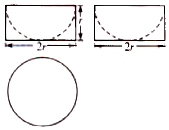 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
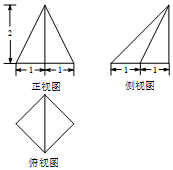
| A. | 2 | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
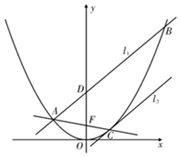 如图,已知过抛物线E:x2=4y的焦点F的直线交抛物线E与A、C两点,经过点A的直线l1分别交y轴、抛物线E于点D、B(B与C不重合),∠FAD=∠FDA,经过点C作抛物线E的切线为l2.
如图,已知过抛物线E:x2=4y的焦点F的直线交抛物线E与A、C两点,经过点A的直线l1分别交y轴、抛物线E于点D、B(B与C不重合),∠FAD=∠FDA,经过点C作抛物线E的切线为l2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com