
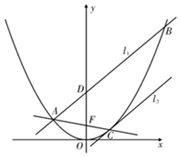
 如图,已知过抛物线E:x2=4y的焦点F的直线交抛物线E与A、C两点,经过点A的直线l1分别交y轴、抛物线E于点D、B(B与C不重合),∠FAD=∠FDA,经过点C作抛物线E的切线为l2.
如图,已知过抛物线E:x2=4y的焦点F的直线交抛物线E与A、C两点,经过点A的直线l1分别交y轴、抛物线E于点D、B(B与C不重合),∠FAD=∠FDA,经过点C作抛物线E的切线为l2.分析 (Ⅰ)设AF的方程为:y=kx+1.设A(x1,y1),C(x2,y2),(不妨设x2>0)由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$得x2-4kx-4=0,⇒x1+x2=4k,x1x2=-4,由∠FAD=∠FDA,得AF=DF,yD=y1+2.即可得k1=k2,可证l1∥l2.
(Ⅱ)由(Ⅰ)得直线l1的斜率为$\frac{1}{2}{x}_{2}$,故直线l1的方程为:$y=\frac{1}{2}{x}_{2}x+\frac{{{x}_{1}}^{2}}{4}+2$
联立$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=\frac{1}{2}{x}_{2}x+\frac{{{x}_{1}}^{2}}{4}+2}\end{array}\right.$得${x}^{2}-2{x}_{2}x-{{x}_{1}}^{2}-8=0$
AB=$\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}•\sqrt{({x}_{1}+{x}_{B})^{2}-4{x}_{1}{x}_{B}}$=2$\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}•\sqrt{({x}_{1}-{x}_{2})^{2}}$,
点C到直线l1的距离为d=$\frac{({x}_{1}-{x}_{2})^{2}}{4\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}}$,三角形ABC面积s=$\frac{1}{2}×AB×d$=$\frac{1}{4}({x}_{2}-{x}_{1})^{3}$,由(Ⅰ)可得${x}_{2}-{x}_{1}=4\sqrt{{k}^{2}+1}$,可得当k=0时,三角形ABC面积s=$\frac{1}{2}×AB×d$=$\frac{1}{4}({x}_{2}-{x}_{1})^{3}$取最小值.
解答 解:(Ⅰ)证明:∵抛物线E:x2=4y的焦点F为(0,1),且直线AF的斜率一定存在,
故设AF的方程为:y=kx+1.
设A(x1,y1),C(x2,y2),(不妨设x2>0)
由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$得x2-4kx-4=0,⇒x1+x2=4k,x1x2=-4,
∵∠FAD=∠FDA,∴AF=DF,${y}_{1}+\frac{p}{2}={y}_{D}-1$,∴yD=y1+2.
∴直线l1的斜率为k1=$\frac{{y}_{D}-{y}_{1}}{{x}_{D}-{x}_{1}}=\frac{2}{-{x}_{1}}$,
∵x1x2=-4,∴${k}_{1}=\frac{2}{-{x}_{1}}=\frac{1}{2}{x}_{2}$
又∵$y′=\frac{1}{2}x$,∴过C(x2,y2)的切线斜率${k}_{2}=\frac{1}{2}{x}_{2}$.
即k1=k2,∴l1∥l2.
(Ⅱ)由(Ⅰ)得直线l1的斜率为$\frac{1}{2}{x}_{2}$,故直线l1的方程为:$y=\frac{1}{2}{x}_{2}x+\frac{{{x}_{1}}^{2}}{4}+2$
联立$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=\frac{1}{2}{x}_{2}x+\frac{{{x}_{1}}^{2}}{4}+2}\end{array}\right.$得${x}^{2}-2{x}_{2}x-{{x}_{1}}^{2}-8=0$,
∴x1+xB=2x2,${x}_{1}{x}_{B}=-({{x}_{1}}^{2}+8)$.
∴AB=$\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}•\sqrt{({x}_{1}+{x}_{B})^{2}-4{x}_{1}{x}_{B}}$=2$\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}•\sqrt{({x}_{1}-{x}_{2})^{2}}$,
点C到直线l1的距离为d=$\frac{\frac{1}{2}{{x}_{2}}^{2}-\frac{{{x}_{2}}^{2}}{4}+\frac{{{x}_{1}}^{2}}{4}+2}{\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}}$=$\frac{\frac{1}{4}{{x}_{2}}^{2}+\frac{1}{4}{{x}_{1}}^{2}+2}{\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}}$=$\frac{\frac{1}{4}({{x}_{1}}^{2}+{{x}_{2}}^{2}+8)}{\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}}$=$\frac{\frac{1}{4}[({x}_{1}-{x}_{2})^{2}+2{x}_{1}{x}_{2}+8]}{\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}}$=$\frac{({x}_{1}-{x}_{2})^{2}}{4\sqrt{1+\frac{1}{4}{{x}_{2}}^{2}}}$
三角形ABC面积s=$\frac{1}{2}×AB×d$=$\frac{1}{4}({x}_{2}-{x}_{1})^{3}$
由(Ⅰ)可得${x}_{2}-{x}_{1}=4\sqrt{{k}^{2}+1}$,所以当k=0时(x2-x1)min=4,
∴当k=0时,三角形ABC面积s=$\frac{1}{2}×AB×d$=$\frac{1}{4}({x}_{2}-{x}_{1})^{3}$取最小值,(s)min=$\frac{1}{4}×{4}^{3}=16$.
点评 本题考查了抛物线的性质,抛物线与直线的位置关系,方程思想、转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}π$ | B. | 16π | C. | $\frac{32}{3}π$ | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
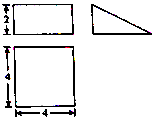
| A. | 32+8$\sqrt{5}$ | B. | 36π | C. | 18π | D. | $\frac{40\sqrt{10}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com