练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在三棱柱ABCA1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：

    (1)B，C，H，G四点共面；

    (2)平面EFA1∥平面BCHG.


    证明：(1)因为GH是△A1B1C1的中位线，

    所以GH∥B1C1.

    又因为B1C1∥BC，所以GH∥BC.

    所以B，C，H，G四点共面．

    (2)因为E、F分别为AB、AC的中点，

    所以EF∥BC.

    因为EF⊄平面BCHG，BC⊂平面BCHG，

    所以EF∥平面BCHG.

    因为A1G綊EB，

    所以四边形A1EBG是平行四边形．

    所以A1E∥GB.

    因为A1E⊄平面BCHG，GB⊂平面BCHG.

    所以A1E∥平面BCHG.

    因为A1E∩EF＝E，

    所以平面EFA1∥平面BCHG.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    命题“，”的否定是       ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图是某个四面体的三视图，该四面体的体积为(　　)

    A．72        B．36        C．24        D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：


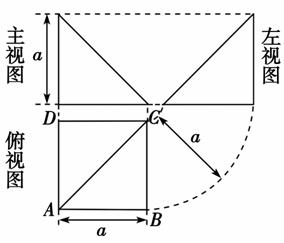
    四棱锥PABCD的顶点P在底面ABCD中的投影恰好是A，其三视图如图所示，根据图中的信息，在四棱锥的任两个顶点的连线中，互相垂直的异面直线对数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如下图，正方体ABCDA1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线　(　　)

    A．不存在　               B．有1条

    C．有2条　               D．有无数条

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个无盖的正方体盒子展开后的平面图如图所示，A、B、C是展开图上的三点，则在正方体盒子中，∠ABC的大小为(　　)

    A．30°              B．45°

    C．60°              D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下四个命题中为真命题的是________(填序号)．

    ①等腰四棱锥的腰与底面所成的角都相等

    ②等腰四棱锥的侧面与底面所成的二面角都相等或互补

    ③等腰四棱锥的底面四边形必存在外接圆

    ④等腰四棱锥的各顶点必在同一球面上

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝(m2－m－1)x－5m－3，m为何值时，f(x)是：

    (1)幂函数？

    (2)幂函数，且是(0，＋∞)上的增函数？

    (3)正比例函数？

    (4)反比例函数？

    (5)二次函数？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝ax3＋bsin x＋9(a，b∈R)，且f(－2 013)＝7，则f(2 013)＝(　　)

    A．11        B．12        C．13        D．14

    查看答案和解析>>

    同步练习册答案