练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知△ABC的内角A，B，C的对边分别为a，b，c且asinA+csinC-
    		3
    asinC=bsinB．
    （1）求角B的大小；
    （2）若A=60°，b=2，求边a，c的大小．
    考点：正弦定理,余弦定理
    专题：解三角形
    分析：（1）由正弦定理得出a2+c2-b2=
    		3
    ac    ，然后由余弦定理即可得出结果；
    （2）首先求出C的度数，然后由正弦定理求出a和c的值即可．
    解答： 解：（1）由正弦定理知，a2+c2-
    		3
    ac=b2    ，
    ∴a2+c2-b2=
    		3
    ac    ，
    由余弦定理得，cosB=
    a2+c2-b2
    2ac
    =
    		3
    2
    ，
    ∴B∈（0°，180°），
    故B=30°，
    （2）∵A+B+C=180°，∴C=180°-（A+B）=180°-（60°+30°）=90°，
    由正弦定理
    a
    sinA
    =
    b
    sinB
    =
    c
    sinC
    ，
    a=
    bsinA
    sinB
    =
    2×
    		3
    2
    1
    2
    =2
    		3
    ，
    c=
    bsinC
    sinB
    =
    2×1
    1
    2
    =4．．
    点评：本题主要考查的是余弦定理和正弦定理，灵活运用定理是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知定义在R上的函数f（x），满足f（x）=f（x+4），f（2+x）=f（2-x），若0＜x＜2时，f（x）=2-x，则f（2015）=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    画出解不等式ax＞b（b≠0）的程序框图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=mx2+2x+10在[4，5]上是增函数，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a，b∈R，则“（a-b）a2＜0”是“a＜b”的（　　）
    A、充分而不必要条件
    B、必要而不充分条件
    C、充要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知一个椭圆中心在原点，对称轴为坐标轴，焦点在x轴上，短轴的一个顶点B与两个焦点F1，F2组成的三角形的周长为4+2
    		3
    ，且∠F1BF2=
    2π
    3
    ．
    （1）求这个椭圆的方程；
    （2）斜率为1的直线交椭圆C于A、B两点，求|AB|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个盒子中装有5个编号依次为1、2、3、4、5的球，这5个球除号码外完全相同，有放回的连续抽取两次，每次任意地取出一个球．
    （1）用列表或画树状图的方法列出所有可能结果；
    （2）设第一次取出的球号码为x，第二次取出的球号码为y，求事件A=“点（x，y）落在直线y=x+1上方”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知△ABC中角A，B，C的对边分别为a，b，c，且
    		3
    sinA-cosA=1．
    （1）求角A的大小；
    （2）若a=2，cosB=
    		3
    3
    ，求b的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

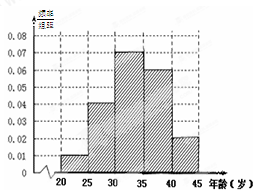    上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．根据如图所示的频率分布直方图，估计这507个画师中年龄不超过30岁的人数约
     
    人（四舍五入精确到整数）．

    查看答案和解析>>

    同步练习册答案