
| OP |
| Sn |
| n |
| OP1 |
| Sm |
| m |
| OP2 |
| Sk |
| k |
| OP |
| OP1 |
| OP2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
| P1P |
| P1P2 |
| OP |
| OP1 |
| P1P |
| OP1 |
| P1P2 |
| OP1 |
| OP2 |
| OP1 |
| OP1 |
| OP2 |
| Sn |
| n |
| n-1 |
| 2 |
| d |
| 2 |
| d |
| 2 |
| Sn |
| n |
| P1P |
| P1P2 |
| OP |
| OP1 |
| P1P |
| OP1 |
| P1P2 |
| OP1 |
| OP2 |
| OP1 |
| OP1 |
| OP2 |
| P1P |
| d |
| 2 |
| P1P2 |
| d |
| 2 |
| n-m |
| k-m |
| n-m |
| k-m |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
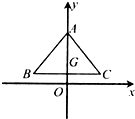 如图,正△ABC的中心位于点G(0,1),A(0,2),动点P从A点出发沿△ABC的边界按逆时针方向运动,设旋转的角度∠AGP=x(0≤x≤2π),向量
如图,正△ABC的中心位于点G(0,1),A(0,2),动点P从A点出发沿△ABC的边界按逆时针方向运动,设旋转的角度∠AGP=x(0≤x≤2π),向量| OP |
| a |
A、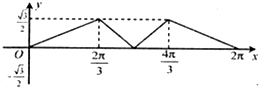 |
B、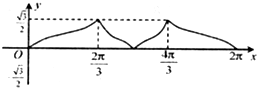 |
C、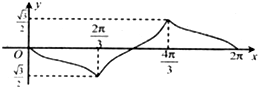 |
D、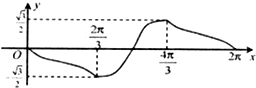 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,圆C:x2+(y-1)2=1与y轴的上交点为A,动点P从A点出发沿圆C按逆时针方向运动,设旋转的角度∠ACP=x(0≤x≤2π),向量
如图,圆C:x2+(y-1)2=1与y轴的上交点为A,动点P从A点出发沿圆C按逆时针方向运动,设旋转的角度∠ACP=x(0≤x≤2π),向量| OP |
| a |
A、 |
B、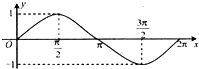 |
C、 |
D、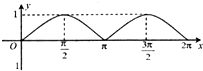 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、660 | B、720 |
| C、780 | D、800 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、70家 | B、50家 |
| C、20家 | D、10家 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AD |
| 1 |
| 3 |
| AC |
| AB |
A、2
| ||
B、
| ||
| C、1 | ||
| D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(-2,0)∪(0,2) |
| B、(-∞,-2)∪(0,2) |
| C、(-2,0)∪(2,+∞) |
| D、(-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 一次购买件数 | 1~10 | 11~50 | 51~100 | 101~300 | 300以上 |
| 每件价格(单位:元) | 37 | 32 | 30 | 27 | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com