
分析 (1)f′(x)=$\frac{1}{x}$-m,(x>0).令g(x)=f′(x)+mx=$\frac{1}{x}$-m+mx,(x>0),(m>0).利用当时研究其单调性极值与最值即可得出.
(2)f′(x)=$\frac{1}{x}$-m,对m分类讨论,利用导数研究函数的单调性极值与最值即可得出.
解答 解:(1)f′(x)=$\frac{1}{x}$-m,(x>0).
令g(x)=f′(x)+mx=$\frac{1}{x}$-m+mx,(x>0),(m>0).
g′(x)=-$\frac{1}{{x}^{2}}$+m=$\frac{m({x}^{2}-\frac{1}{m})}{{x}^{2}}$=$\frac{m(x+\sqrt{\frac{1}{m}})(x-\sqrt{\frac{1}{m}})}{{x}^{2}}$,
当x>$\sqrt{\frac{1}{m}}$时,g′(x)>0,此时函数g(x)单调递增;
当0<x<$\sqrt{\frac{1}{m}}$时,g′(x)<0,此时函数g(x)单调递减.
∴当x=$\sqrt{\frac{1}{m}}$时,函数g(x)取得极小值,即最小值.
∴f′(x)+mx的最小值为g$(\sqrt{\frac{1}{m}})$=$\sqrt{m}$-m+m$•\sqrt{\frac{1}{m}}$=2$\sqrt{m}$-m.
(2)f′(x)=$\frac{1}{x}$-m,
①当m≤0时,f′(x)>0恒成立,则函数f(x)在(0,+∞)上单调递增,
f(1)=0,因此:f(x)>0在x∈(0,+∞)上有解.
②当m>0时,由f′(x)=$\frac{1}{x}$-m=$\frac{-m(x-\frac{1}{m})}{x}$,得x∈$(0,\frac{1}{m})$,f′(x)>0,
此时f(x)的单调递增区间为$(0,\frac{1}{m})$,单调递减区间为$(\frac{1}{m},+∞)$;
当m>0时,f(x)max=$f(\frac{1}{m})$=-lnm-1+m.
令g(x)=x-lnx-1,
则g′(x)=1-$\frac{1}{x}$,x∈(0,+∞)
得函数g(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
∴g(x)min=g(1)=0,g(x)≥0对x∈(0,+∞)恒成立,
也就是m-lnm-1≥0对m∈(0,+∞)恒成立.
∴m>0,m≠1时,m-lnm-1>0对m∈(0,+∞)恒成立.
综上①②可得:m≠1时,f(x)>0在x∈(0,+∞)上有解,
可得:实数m的取值集合M={m|m≠1}.
点评 本题考查了利用导数研究函数的单调性极值与最值、分类讨论方法、不等式的解法,考查了推理能力与计算能力,属于难题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,且P、Q不是正方体的顶点,则|PR|的最小值是( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,且P、Q不是正方体的顶点,则|PR|的最小值是( )| A. | $\frac{{\sqrt{42}}}{6}$ | B. | $\frac{{\sqrt{30}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
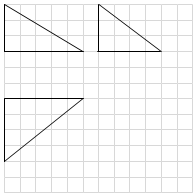 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )| A. | 25π | B. | 50π | C. | 75π | D. | 100π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )
如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸,若该多面体的顶点在同一球面上,则该球的表面积等于( )| A. | 8π | B. | 18π | C. | 24π | D. | 8$\sqrt{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
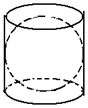 如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )| A. | 2R | B. | $\frac{4R}{3}$ | C. | $\frac{2}{3}R$ | D. | $\frac{R}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<$\frac{1}{3}$ | B. | a≥$\frac{1}{3}$ | C. | a>$\frac{1}{3}$ | D. | 0<a<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
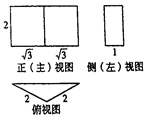
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com