
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,求
,求![]() 的极大值;
的极大值;
(3)若![]() ,指出
,指出![]() 的零点个数.
的零点个数.
【答案】(1)![]() 的单调减区间为
的单调减区间为![]() ;(2)
;(2)![]() 的极大值为
的极大值为![]() (3)
(3)![]() 时,
时, ![]() 的零点个数为0;当
的零点个数为0;当![]() 时,
时, ![]() 的零点个数为1.
的零点个数为1.
【解析】试题分析:(1)求导函数,解不等式![]() (或
(或![]() )即可求解;(2)求导后分析导数何时取正,何时取负,当在
)即可求解;(2)求导后分析导数何时取正,何时取负,当在![]() 处左正右负时,
处左正右负时, ![]() 即为所求;(3)分
即为所求;(3)分![]() 和
和![]() 两种情况讨论,当
两种情况讨论,当![]() 时易知最小值大于0,故无解,当
时易知最小值大于0,故无解,当![]() 时,对m分区间讨论即可.
时,对m分区间讨论即可.
试题解析:(1)![]() 时,则
时,则![]() ,∴
,∴![]() .
. ![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,
, ![]() 的单调减区间为
的单调减区间为![]() .
.
(2)![]() 时,
时, ![]() ,
, ![]() ,设
,设![]() .
.
![]() ,∴
,∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
又![]() ,∴
,∴![]() 的极大值为
的极大值为![]() .
.
(3)当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,此时
,此时![]() 的零点个数为0.
的零点个数为0.
当![]() 时,
时, ![]() .
.
若![]() ,
, ![]() ,
, ![]() 无解;
无解;
若![]() ,
, ![]() ,即
,即![]() ,在
,在![]() 上
上![]() ,
,
在![]() 上
上![]() 单调递增,
单调递增, ![]() 单调递减,且
单调递减,且![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() 有且仅有一解.
有且仅有一解.
∴当![]() 时,
时, ![]() 的零点个数为1.
的零点个数为1.
综上可得, ![]() 时,
时, ![]() 的零点个数为0;当
的零点个数为0;当![]() 时,
时, ![]() 的零点个数为1.
的零点个数为1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知几何体P﹣ABCD如图,面ABCD为矩形,面ABCD⊥面PAB,且面PAB为正三角形,若AB=2,AD=1,E、F分别为AC、BP中点,
(Ⅰ)求证:EF∥面PCD;
(Ⅱ)求直线BP与面PAC所成角的正弦值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() 与
与 ![]() 的夹角为120°,且|
的夹角为120°,且| ![]() |=4,|
|=4,| ![]() |=2,
|=2,
(1)求 ![]()
![]() ;
;
(2)求|3 ![]() +5
+5 ![]() |;
|;
(3)若向量 ![]() +k
+k ![]() 与5
与5 ![]() +2
+2 ![]() 垂直,求实数k的值.
垂直,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足c cosB=(2a+b)cos(π﹣C).
(1)求角C的大小;
(2)若c=4,△ABC的面积为![]() ,求a+b的值
,求a+b的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 在R上可导,其导函数为
在R上可导,其导函数为 ![]() 且函数
且函数 ![]() 的图像如图所示,则下列结论一定成立的是( )
的图像如图所示,则下列结论一定成立的是( ) 
A.函数 ![]() 的极大值是
的极大值是 ![]() ,极小值是
,极小值是 ![]()
B.函数 ![]() 的极大值是
的极大值是 ![]() ,极小值是
,极小值是 ![]()
C.函数 ![]() 的极大值是
的极大值是 ![]() ,极小值是
,极小值是 ![]()
D.函数 ![]() 的极大值是
的极大值是 ![]() ,极小值是
,极小值是 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.


(1)求![]() 的值;
的值;
(2)该校决定在成绩较好的3、4、5组用分层抽样抽取6名学生进行面试,则每组应各抽多少名学生?
(3)在(2)的前提下,已知面试有4位考官,被抽到的6名学生中有两名被指定甲考官面试,其余4名则随机分配给3位考官中的一位对其进行面试,求这4名学生分配到的考官个数![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点在x轴上,短轴长为4,离心率为 ![]() .
.
(1)求椭圆的标准方程;
(2)若直线l过该椭圆的左焦点,交椭圆于M、N两点,且 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
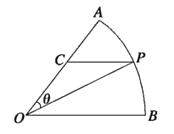
【题目】如图所示,扇形![]() ,圆心角
,圆心角![]() 的大小等于
的大小等于![]() ,半径为2,在半径
,半径为2,在半径![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作平行于
作平行于![]() 的直线交弧
的直线交弧![]() 于点
于点![]() .
.
(1)若![]() 是半径
是半径![]() 的中点,求线段
的中点,求线段![]() 的大小;
的大小;
(2)设![]() ,求
,求![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com