
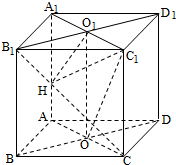
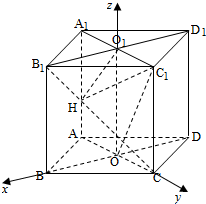
 如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.| 3 |
| 3 |
| 3 |
| n1 |
| n2 |
|
|
| 3 |
| 3 |
| n2 |
| 3 |
| 3 |
| n1 |
| n2 |
| ||||
|
|
2
| ||
|
2
| ||
| 19 |
2
| ||
| 19 |


科目:高中数学 来源: 题型:
A、
| ||
| B、2 | ||
| C、3 | ||
| D、1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| a |
| OM |
| OA |
| OB |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| k |
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
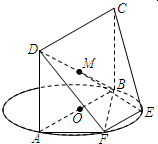 如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=
如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
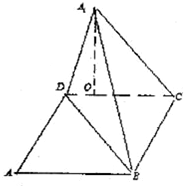 如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.
如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.查看答案和解析>>
科目:高中数学 来源: 题型:
| 分组 | [0,1) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 频率 | 0.1 | 0.18 | 0.22 | 0.25 | 0.2 | 0.05 |
| 非网迷 | 网迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
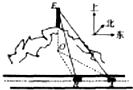 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com