Question

14．已知动圆M经过点A（-2，0），且与圆B：（x-2）²+y²=4相内切（B为圆心）．
（1）求动圆的圆心M的轨迹C的方程；
（2）过点B且斜率为2的直线与轨迹C交于P，Q两点，求△APQ的周长．

Answer 1

分析 （1）由两圆相内切的条件可得|，|MB|=|MT|-|BT|=|MA|-2，再由双曲线的定义，可得M的轨迹为以A，B为焦点的双曲线的右支，且c=2，a=1，b=$\sqrt{3}$，即可得到所求轨迹方程；
（2）求出直线方程，代入双曲线的方程，运用韦达定理和弦长公式，求得|PQ|，再由双曲线的定义可得△APQ的周长为4a+2|PQ|，计算即可得到所求周长．

解答 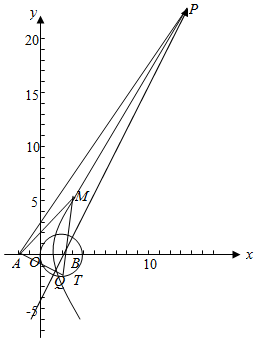解：（1）动圆M经过点A（-2，0），
且与圆B：（x-2）²+y²=4相内切（B为圆心），
可得|MA|=|MT|，|MB|=|MT|-|BT|=|MA|-2，
|MA|-|MB|=2＜|AB|=4，
由双曲线的定义可得，
M的轨迹为以A，B为焦点的双曲线的右支，且c=2，a=1，b=$\sqrt{3}$，
即有动圆的圆心M的轨迹C的方程为x²-$\frac{{y}^{2}}{3}$=1（x＞0）；
（2）过点B且斜率为2的直线方程为y=2x-4，
代入双曲线的方程x²-$\frac{{y}^{2}}{3}$=1，可得x²-16x+19=0，
设P（x₁，y₁），Q（x₂，y₂），
可得x₁+x₂=16，x₁x₂=19，
则|PQ|=$\sqrt{1+{2}^{2}}$•$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{5}$•$\sqrt{1{6}^{2}-4×19}$=30，
则△APQ的周长为|AP|+|PB|+|BQ|+|AQ|
=2a+2|PB|+2|BQ|+2a=4a+2|PQ|=4+60=64．

点评 本题考查双曲线的定义和方程的运用，考查两圆的位置关系，主要是内切的条件，考查直线方程和双曲线的方程联立，运用韦达定理和弦长公式，考查运算能力，属于中档题．