
分析 (1)直接由题意可得|CQ|+|AQ|=4>|AC|=2$\sqrt{3}$,符合椭圆定义,且得到长半轴和半焦距,再由b2=a2-c2求得b2,则点Q的轨迹方程可求;
(2)设M(x1,y1),N(x2,y2),由题意可设直l的方程为:y=kx-2,与椭圆的方程联立可得根与系数的关系,再利用三角形的面积计算公式即可得出S△OMN.通过换元再利用基本不等式的性质即可得出.
解答 解:(1)由题意知|PQ|=|AQ|,
又∵|CP|=|CQ|+|PQ|=4…(2分)
∴|CQ|+|AQ|=4>|AC|=2$\sqrt{3}$
由椭圆定义知Q点的轨迹是椭圆,a=2,c=$\sqrt{3}$…(3分)
∴b=1,
∴点Q的轨迹E的方程$\frac{{x}^{2}}{4}+{y}^{2}$=1.…(5分)
(2)由题意知所求的直线不可能垂直于x轴,所以可设直线为:y=kx-2,M(x1,y1),N(x2,y2),
联立方程组,将y=kx-2代入$\frac{{x}^{2}}{4}+{y}^{2}$=1得(1+4k2)x2-16kx+12=0…(6分)
当△>0时,即k2>$\frac{3}{4}$时,x1+x2=$\frac{16k}{1+4{k}^{2}}$,x1x2=$\frac{12}{1+4{k}^{2}}$,…(7分)
则△OMN的面积S=$\frac{1}{2}$|OB||x1-x2|=$\frac{4\sqrt{4{k}^{2}-3}}{1+4{k}^{2}}$…(8分)
设$\sqrt{4{k}^{2}-3}$=t>0,
∴${S_{△OMN}}=\frac{4t}{{{t^2}+4}}=\frac{4}{{t+\frac{4}{t}}}≤1,当且仅当t=\frac{4}{t}即t=2时面积最大$,最大值为1…(10分)
∴$\sqrt{4{k}^{2}-3}$=2,k=±$\frac{\sqrt{7}}{2}$,满足△>0…(11分)
∴直线的方程为y=±$\frac{\sqrt{7}}{2}$x-2…(12分)
点评 本题综合考查了椭圆的标准方程及其性质、椭圆的方程联立可得根与系数的关系、三角形的面积计算公式、基本不等式的性质等基础知识与基本技能方法,考查了推理能力和计算能力,考查了换元法和转化方法,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | A>B>C | B. | A>C>B | C. | B>A>C | D. | C>B>A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006+22017 | B. | 1010+22016 | C. | 1006+22016 | D. | 2014+22017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 050 | B. | 051 | C. | 052 | D. | 053 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
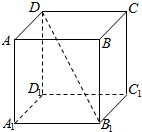
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (13,49) | B. | [2,2+$\sqrt{13}$] | C. | [2,13] | D. | [4,22+6$\sqrt{13}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com